42: La question de la vie de l'univers et du reste, en moins de 7,5 millions d'années
6. Space Opéra
Lorsque l’on tente d’imaginer la création de l’univers, l’espace et le temps semblent y jouer un rôle primordial. Ces deux notions paraissent tellement fondamentales que, s’il est encore possible de concevoir un univers totalement vide avant sa naissance, il est beaucoup plus difficile de se représenter que temps et espace n’y existaient pas préalablement. Comment parler de la création si celle-ci ne survient pas à un moment donné et à un endroit précis ? Nous pouvons alors nous poser la question de savoir si tout ce beau monde est apparu conjointement, ou si l’univers a émergé dans un espace-temps lui préexistant. Celui-ci était-il là à guetter patiemment l’étincelle de la création venant mettre le feu aux poudres ? telle une salle de théâtre vide attendant que les acteurs entrent en piste. Ce que nous allons voir dans ce chapitre, c’est qu’aucune de ces deux options n’est la bonne : temps et espace ne se présentent pas comme des propriétés fondamentales prévalant sur l’univers. Ce ne sont que des phénomènes qui en ont émergé lors de son évolution.
Vers l’infini et au-delà ?
Einstein est l’auteur de la célèbre citation : « Deux choses sont infinies : l’Univers et la bêtise humaine. Mais, en ce qui concerne l’Univers, je n’en ai pas encore acquis la certitude absolue. » En ce qui me concerne, j’émets beaucoup moins de doute. Je suis persuadé que l’infini se limite à un concept mathématique et que rien s’en approchant n’existe, en tout cas pas dans l’univers où nous sommes. Au risque d’énoncer une lapalissade, le problème avec l’infini, c’est que c’est grand, tellement grand que ça conduit à toutes sortes de paradoxes. S’ils s’avèrent communs en mathématique, force est de constater que le monde que nous habitons semble en être totalement dépourvu. À mes yeux, toutes les lois physiques nous indiquent qu’absolument tout est borné et mesurable. Au mieux, l’infini apparaît comme un faux semblant trahissant le gigantisme de notre univers. Mais malgré le fait que sa taille nous dépasse complètement, il n’en demeure pas moins que le monde que nous habitons présentent toutes les caractéristiques d’une entité finie.
Pour vous donner le goût de ce à quoi correspond l’infini, nous pouvons partir d’un nombre plutôt grand au regard de ce que nous côtoyons habituellement. Ce nombre porte le nom de googol et est à l’origine de l’appellation de la firme Google. Sa valeur est fixée à 10100, soit un 1 suivi de 100 zéros. Pour cerner ce que représente une telle taille, nous pouvons essayer de le comparer à d’autres choses : par exemple, le nombre de molécules contenues dans un verre d’eau tourne autour de 1025. Si la terre n’était composée que de sable, elle enfermerait environ 1033 grains. Quant aux atomes qui rentrent dans la constitution de la terre, ils s’élèvent au nombre de 1050. Finalement, le nombre de particules dans l’univers observable est estimé à 1080.
Toutes ces valeurs volent toujours en dessous du googol. Pour tenter de le surpasser, nous pouvons compter le nombre de volumes de Planck nécessaires pour remplir l’univers observable. La longueur de Planck correspond à la plus petite longueur en dessous de laquelle les physiciens pensent que la notion d’espace perde son sens, elle vaut approximativement 10-35 mètres. En considérant un volume de Planck comme un petit cube dont les arrêtes mesurent cette taille, nous en arrivons au bout du compte à un univers constitué de 10183 de ces petits volumes.
Mais ces nombres se révèlent finalement désuets face à la puissance de l’infini. Comme l’a présenté Brady Haran sur sa chaîne Youtube Numberphile, essayons d’imaginer quelque chose incroyablement plus grand, comme le googolplex. Ce nombre ne dispose d’aucune particularité en soi, hormis le fait d’avoir reçu un nom. Sa valeur est égale à 10googol, soit 1010100. Vous éprouveriez bien de la peine si vous deviez écrire ce nombre dans le système décimal. Il est en effet constitué d’un 1 suivi de 10100 zéros, soit plus de zéros que de particules dans l’univers. Même si un googolplex reste petit face à l’infini, essayons tout de même de nous imaginer en train d’arpenter un univers de cette taille, mesurée en mètres.
Dans ce contexte, prenons un volume de 100 litres, soit à peu de choses près l’encombrement d’un être humain. Par de savants calculs, il y a moyen d’estimer le nombre de configurations quantiques avec lesquelles il est possible d’agencer un tel volume d’espace [25]Ce calcul se base sur l’entropie S d’un trou noir de surface A et donné par la formule S=(k.A) / (4.lp2). Dans celle-ci, k est la constante de Bolzmann et lp est la longueur de Planck. Cette entropie est liée au nombre d’états possibles N par la formule S=k.log(N). . Toutes ces configurations représentent tout ce que nous pouvons imaginer. Par exemple, ce volume pourrait correspondre à du caillou, à du vide, à de l’hydrogène en fusion comme il en existe au cœur d’une étoile, à un être humain, à un ordinateur… Elle pourrait concrètement coïncider avec tout ce que nous pouvons trouver d’autre dans un volume de 100 litres d’univers. Il se trouve que le nombre d’états envisageables pour un tel volume tourne autour de 101070 configurations, soit un nombre bien inférieur au googolplex. Ce résultat signifie que, comme cet hypothétique univers contiendrait beaucoup plus de volumes de 100 litres que de configurations imaginables pour ce même volume, certaines parties de l’univers devraient immanquablement se répéter et n’afficher aucune différence entre elles. En conséquence, vous pourriez considérer que votre propre personne, en tant que l’une des configurations possibles de 100 litres d’univers, puisse exister en plusieurs exemplaires identiques en différents endroits du cosmos. Imaginer un univers infini, c’est ouvrir tout grand la porte à ce genre de paradoxes.
Tout nous incite toutefois à penser que ce genre de scénario ne peut se produire. Prenons un exemple flagrant tel que la vitesse de la lumière, valant approximativement 300.000 km/s. Cette vitesse constitue une limite physique infranchissable et nous pourrions a priori nous demander pourquoi. Pour répondre à cette question, il est d’abord intéressant de remarquer que cette valeur semble un peu arbitraire. Pourquoi 300.000 et pas autre chose. Ce côté arbitraire provient en fait de sa définition basée sur celle du mètre et de la seconde. Or il se trouve que ces deux unités ont été établies pour leur usage pratique à l’échelle humaine et sont donc un peu déconnectées de la physique. Max Planck fut le premier à définir ce que l’on appelle les unités de Planck, ou unités naturelles. Dans ce système de mesure, Planck retira tous les éléments arbitraires pour ne laisser subsister que des constantes fondamentales. La plus petite distance qui revêt un sens physique dans ce système s’applique à la longueur de Planck (1.6 10-35 m) et celle-ci est définie comme valant 1. De la même manière, le plus petit intervalle de temps qui produit du sens s’appelle la durée de Planck (5.10-44 s), pareillement établie à la valeur 1. Sur base de cette nouvelle référence, la durée de Planck correspond précisément au temps nécessaire à un photon pour traverser une distance d’une longueur de Planck. Dès lors, la vitesse de la lumière dans ce système d’unités vaut exactement 1.
Une vitesse maximale de 1 semble effectivement plus naturelle. Mais pour encore mieux se rendre compte de ce qui se cache derrière, je vais à nouveau réaliser un parallélisme avec la programmation d’un jeu vidéo. Si vous vous essayez à cet exercice, il vous faudra obligatoirement discrétiser le temps et l’espace. Cette étape implique de définir le plus petit intervalle d’espace utilisable par vos unités ou personnages pour se déplacer, ainsi que l’incrément de temps qui s’écoulera chaque fois que vous calculerez le nouvel état du monde sur base du précédent. Cette discrétisation, indispensable, découle du constat que la représentation d’un espace et d’un temps continus conduit inévitablement à se heurter à des infinis.
En effet, la plage mémoire d’un ordinateur est limitée et il n’est pas réaliste de travailler avec des nombres arbitrairement précis. Plus un nombre dispose d’une grande précision, plus la quantité de Bytes d’information requis pour le représenter est élevée. Aussi serez-vous bien obligé en pratique de définir la plus petite mesure d’espace manipulable et de ne travailler qu’avec des multiples de cette valeur. De la même manière, la capacité de traitement d’un ordinateur est finie. Cette limitation implique que vous ne pourrez calculer l’évolution du jeu entre deux instants qu’en un nombre fini d’étapes. Chaque transition coûte du temps de calcul, et vous serez forcés de définir l’incrément de temps non nul à utiliser pour faire évoluer le jeu pas à pas.
Nous en arrivons maintenant à un problème bien gênant et survenant lors de la programmation d’un moteur physique de jeu vidéo. Ce problème apparaît dès qu’un objet est autorisé à se déplacer plus vite qu’une unité d’espace par unité de temps, un peu comme s’il dépassait la vitesse de la lumière dans son contexte. À titre d’exemple, considérons un jeu représenté par une grille discrète désignant les différents emplacements où nous pouvons effectivement placer nos objets. Imaginons ensuite disposer d’un personnage et d’un mur séparés par une dizaine de cases et que ce protagoniste décide de tirer en direction de cet élément du décor (Figure 7). Si la vélocité du projectile est élevée, elle pourrait se manifester par un déplacement de cinq cases ou plus à chaque pas de temps. Dès lors, si un programmeur devait implémenter naïvement une détection de collision en se basant seulement sur le contenu des cases adjacentes à l’élément en mouvement, le projectile aurait toutes les chances de traverser le mur sans qu’aucune détection soit décelée. Le jeu présenterait donc un problème de causalité, car la ligne de vie du projectile croiserait celle des obstacles sans interagir avec eux.
La correction de ce problème se traduit bien souvent par des pirouettes algorithmiques supplémentaires pour traiter le cas des objets rapides dans un jeu. Ces pirouettes reviennent en fin de compte à regarder plus finement la trajectoire du projectile entre deux positions. Mais ces désagréments ne surviendraient pas si la vitesse maximale de n’importe quel objet ne pouvait pas dépasser 1. Dans ce cas, l’examen purement local de l’état des cases adjacentes suffirait à résoudre toutes les situations de collision, pour toutes les vitesses permises de l’objet considéré. Aussi, s’arranger pour que la vitesse de tout objet ne puisse pas dépasser une certaine limite, que nous pouvons appeler vitesse de causalité, résout efficacement un problème surgissant de la représentation finie des constituants du jeu vidéo. Cette disposition empêche également qu’une vitesse puisse devenir arbitrairement grande et qu’elle ne tienne plus dans la limite mémoire fixée pour décrire une telle variable.
Sans qu’il existe encore de certitude pour le moment, les théories physiques actuelles et les spéculations sur les prochaines avancées me donnent l’impression que l’univers dans lequel nous baignons semble bien obéir aux mêmes genres de limites que notre jeu vidéo. Mon exemple se veut bien sûr simpliste et l’univers n’est certainement pas constitué d’une grille rudimentaire [26]Celle-ci aurait pour effet d’offrir des directions privilégiées le long de ses axes, alors que l’espace est connu pour être isotrope. . Mais ce que nous pouvons observer de l’univers contient un nombre fini d’étoiles et de particules et la vitesse de la lumière est bornée afin de ne pas se confronter à l’infini à quelque niveau que ce soit. Aussi existerait-il une plus petite unité de temps, d’espace ou d’énergie. De la même façon, il y aurait une limite à la quantité d’énergie pouvant être contenue dans un volume donné, comme dans le cas d’un trou noir.
La formidable théorie de la relativité générale développée par Einstein n’a pas encore été prise en défaut dans son domaine d’application. Pourtant, elle souffre de limitations rédhibitoires l’empêchant de couvrir tous les champs de la physique et devra un jour laisser sa place à une « théorie du tout » plus générale, car elle ne permet pas de décrire ce qui se passe aux petites échelles de la matière, où tout est dicté par la mécanique quantique. Cette limitation provient de l’hypothèse que l’espace forme une entité homogène et continue, incompatible avec les quantas de cette seconde théorie. Car à l’échelle des particules, tout se trouve sous l’emprise de ces fameux quantas, c’est-à-dire de propriétés ne pouvant prendre de valeur que par multiples de quantités fondamentales.
Une analogie peut être facilement tracée ici avec la mécanique des fluides. Celle-ci considère les fluides comme des entités continues, régies par des équations différentielles non linéaires portant le nom d’équations de Navier-Stokes. Mais un fluide ne revêt un aspect continu qu’en apparence, c’est-à-dire quand il n’est pas observé de trop près. À petite échelle, un fluide est constitué de molécules discrètes pour lesquelles les équations de Navier-Stokes n’ont aucun sens. Par contre, si le nombre de ces molécules devient suffisant, la nature discrète du processus s’estompe par le moyennage du comportement de chaque entité individuelle, ne laissant finalement la place qu’à une dynamique continue et homogène décrite par ces fameuses équations.
La relativité générale considère aussi l’espace-temps comme homogène et continu, mais cette représentation, couplée à l’ignorance des effets quantiques, a pour conséquence qu’elle ne peut pas prédire certaines quantités mathématiques dans certaines conditions extrêmes. Ce qu’il se passe à l’intérieur d’un trou noir est par exemple inconnu, car plusieurs valeurs calculées par cette théorie deviennent infinies dans cette région de l’univers.
Pour moi, c’est exclusivement en abandonnant toute vision continue du monde qu’il sera un jour possible de concilier tous les points de vue en une théorie unique. Mais la tâche semble ardue, car d’après les modèles actuels, c’est seulement aux alentours de la longueur de Planck, soit 10-35 m, que l’espace commencerait à perdre son aspect homogène et lisse. Or une si infime distance se tapit bien en dessous de la précision de nos meilleurs instruments de mesure. Si vous avez du mal à imaginer ce qu’une si petite dimension signifie, dites-vous que la longueur de Planck est à l’épaisseur d’un cheveu ce que l’épaisseur d’un cheveu est à la taille de l’univers observable. Je trouve que cette comparaison aide quelque peu à se rendre compte du gigantisme incommensurable de ce dernier, fût-il discret.
Émergence de l’espace
Quand j’ai découvert la théorie du Big Bang lorsque j’étais enfant, je me souviens avoir eu beaucoup de mal à me figurer l’analogie du ballon en expansion. Celle-ci présente l’univers comme contenu sur l’enveloppe d’une baudruche et le Big Bang similaire à souffler à l’intérieur de celui-ci. Le gonflement qui en résulte a alors pour effet de distendre l’espace en augmentant la distance qui sépare chaque élément imprimé sur sa surface. Par exemple, si vous dessinez deux points disjoints d’un centimètre sur le ballon dégonflé, puis que vous soufflez à l’intérieur, la distance entre ces deux points va croître, à l’image de l’expansion de l’univers. Bien sûr, l’univers s’exprime en trois dimensions, contrairement à la surface bidimensionnelle considérée ici, mais le principe reste le même.
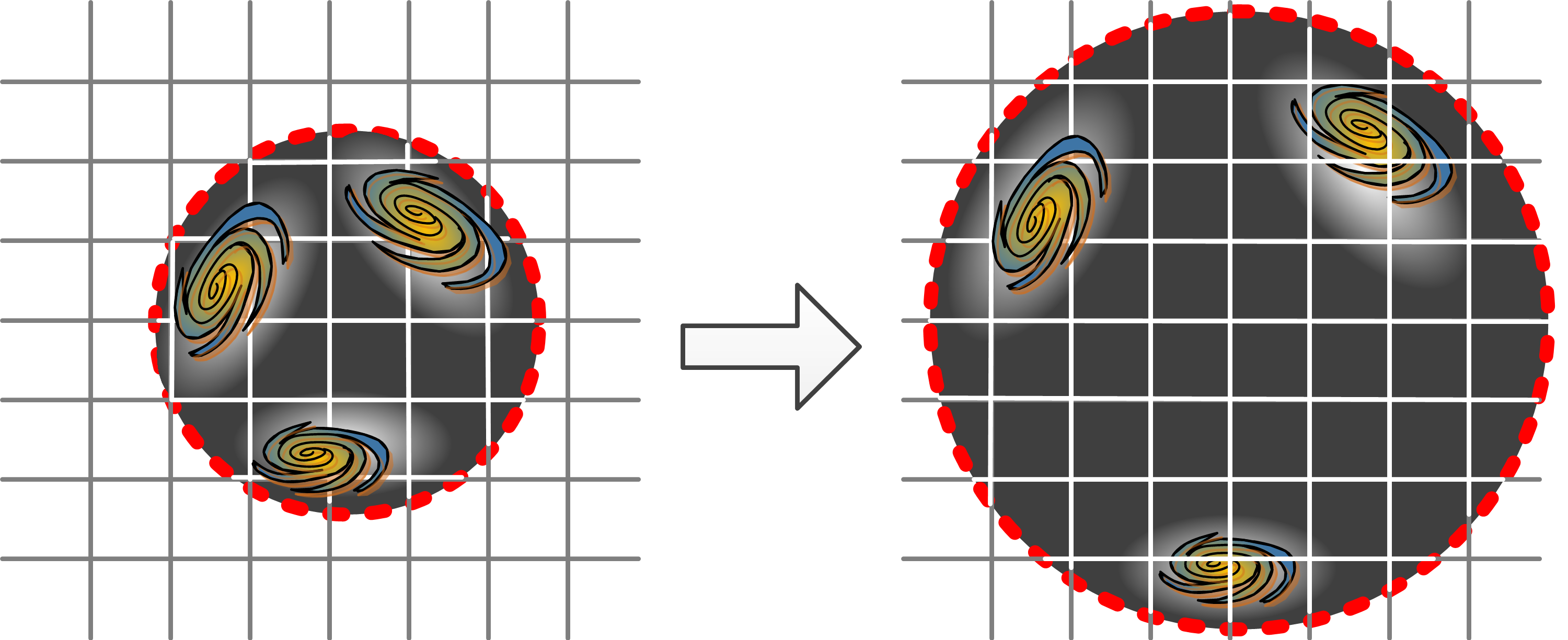
Mon problème de compréhension provenait du fait que je visualisais le ballon à l’intérieur de l’espace lui-même. Comme l’espace contenait le ballon, ce dernier était doté d’un dedans et d’un dehors, et c’est en soufflant à l’intérieur qu’il pouvait croître. Dans ma conception, l’espace jouait le rôle d’arrière-plan s’étendant à l’infini dans toutes les directions. Cette vision substantielle de l’espace, en ce sens qu’il existerait indépendamment de tout objet physique, correspond à celle qu’entretenait Newton. Il identifiait l’espace et le temps à une immense scène de théâtre sur laquelle les acteurs, composés de matière et d’énergie, prenaient vie. Cette scène est représentée par le quadrillage sur l’image ci-dessous (Figure 8).
Notre intuition, basée sur notre expérience de tous les jours, nous laisse penser que le temps et l’espace présentent un aspect lisse et linéaire s’étendant indéfiniment dans toutes les directions. Cette tendance provient du fait que nous n’en observons qu’une infime partie et que nous en extrapolons spontanément le reste sur base du peu que nous en expérimentons. Mais notre intuition a mainte fois révélé qu’elle fonctionnait bien mal dès lors que nous voulions l’appliquer à des phénomènes qui sortent de nos champs d’expérimentation habituels. Notre vision s’en trouve biaisée et laisse la porte ouverte à la question de la nature de l’espace lui-même, ainsi qu’à comment il serait apparu ? L’espace, même vide, ne peut s’identifier au néant, car il dispose à tout le moins de la propriété de pouvoir accueillir la matière d’un univers à venir.
Il existe toutefois une seconde façon d’appréhender l’espace, beaucoup plus élégante; elle consiste à ne pas postuler son existence à priori, mais plutôt de le considérer comme le résultat émergeant de la relation qu’entretiennent les objets physiques entre eux. Ce qu’il faut alors comprendre, une fois appliquée à l’analogie du ballon, c’est que l’espace n’existe qu’au niveau de sa surface. De ce fait, celui-ci n’a pas de dedans ou dehors, et il n’y a rien qui souffle à l’intérieur. Il n’existe pas non plus d’arrière-plan infini pour le contenir, l’univers n’est que la surface finie du ballon. La matière renfermée dans l’univers définit les propriétés de l’espace et en imprime la courbure à l’origine de la gravitation. L’espace, lui, dicte à la matière comment se mouvoir en fonction de sa courbure. Mais sans matière il n’y a pas d’espace, et inversement. Il n’y a donc rien pour contenir le fameux ballon, il se suffit à lui-même et l’univers devient sa propre scène de théâtre (Figure 9).
Ces notions d’espace et de courbure se conceptualisent difficilement, mais encore une fois, je pense que cette limite provient surtout de la vision que nous en avons, c’est-à-dire d’un continuum homogène. Pour illustrer l’un des problèmes que ce point de vue peut engendrer, nous pouvons ressortir un grand classique qui a énormément intrigué les physiciens qui l’ont découvert, et qui continue d’intriguer aujourd’hui, celui de l’intrication quantique.
Sans entrer dans les détails, la mécanique quantique prévoit que deux particules peuvent être intriquées. Cette propriété signifie qu’elles sont en mesure d’être placées conjointement dans une superposition d’états et que, de ce fait, les deux particules constituent momentanément une seule et même entité. Reprenons par exemple les qubits du chapitre précédent. Deux qubits pourraient être intriqués en les plaçant dans la superposition d’états « 00 » et « 11 » à égale probabilité, signifiant que les deux qubits seraient soit tous les deux à « 0 », soit tous les deux à « 1 ». Mesurer l’état de l’un des qubits devra dès lors produire l’état « 0 » ou « 1 » à chances égales; par contre, la mesure du second qubit donnera toujours le même résultat que celui obtenu sur le premier qubit. L’expérience a été maintes fois menée et maintes fois vérifiée. Quel que soit le qubit mesuré en premier, il dispose d’une chance sur deux de se révéler dans l’un ou l’autre état. Mais la mesure du second qubit, elle, donne toujours le même résultat que celui obtenu sur son homologue durant la première mesure. Une telle coïncidence ne peut s’expliquer par le hasard. Tout se passe comme si, une fois mesuré, le premier qubit pouvait envoyer un signal à son jumeau pour lui indiquer vers quel état il devait lui aussi basculer.
Ce qu’il y a de choquant dans cette intrication, c’est qu’il est possible de s’arranger pour que les deux qubits soient très éloignés l’un de l’autre lorsque leur état est mesuré. Cela implique que, moyennant le bon minutage, cet éloignement peut empêcher toute communication de l’un vers l’autre à une vitesse inférieure à celle de la lumière durant l’opération de mesure. Le paradoxe provient ensuite de la capacité des deux qubits à agir comme une seule et même chose, malgré la distance interdisant toute communication qui permettrait leur synchronisation. Aussi ce comportement apparaît-il en contradiction flagrante avec la vision einsteinienne classique que nous avons de l’espace. Il viole le principe de localité qui stipule qu’une particule ne peut être influencée que par ce qui se trouve dans son environnement immédiat. Mais avec l’intrication, tout se passe comme si deux points éloignés de l’espace se situaient en fait au même endroit, ce qui constitue clairement une singularité par rapport à la vision homogène de la théorie de la relativité générale.
Il y a toutefois moyen d’imaginer d’autres structures de l’espace-temps permettant de mieux discerner le mécanisme à l’œuvre dans l’intrication quantique, tout en conservant l’aspect homogène et lisse observé la plupart du temps. C’est par exemple ce à quoi s’essaie la gravitation quantique à boucles, cherchant à unifier certains concepts de la relativité et de la physique quantique. Sans entrer dans les détails d’une telle théorie, je me contenterai ici d’un modèle plus simple, même s’il n’a aucune valeur scientifique. Son seul but vise à montrer que d’autres idées peuvent être imaginées et qu’elles pourraient à terme déboucher sur une vraie « théorie du tout ».
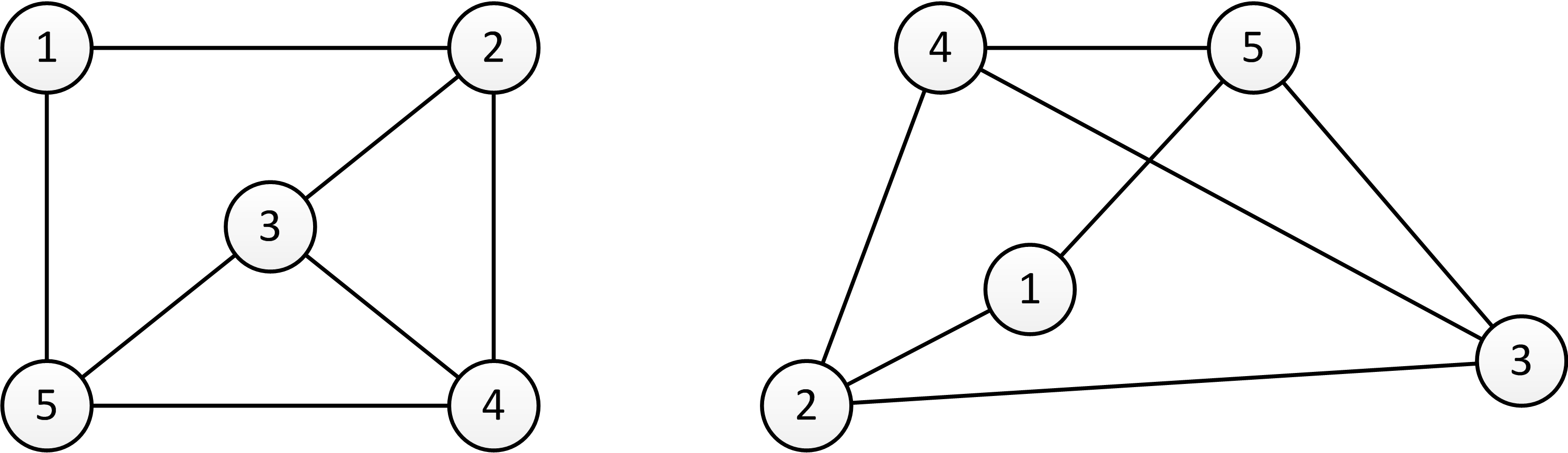
Le principe consiste à considérer un espace discret, non pas comme une grille, mais plutôt comme un graphe dans lequel chaque nœud correspondrait à une unité fondamentale d’espace. Un nœud peut donc être vu comme l’équivalent d’une case d’un tableau, à la différence près que les entités voisines ne sont pas fixées a priori mais peuvent se reconfigurer librement. La notion de « nœud voisin » est en effet symbolisée par un arc joignant un nœud à un autre. Ainsi est-il possible dans cet exemple d’envisager toutes sortes de réseaux à la topologie distincte pour un même nombre de nœuds de départ. Chaque réseau correspond à un câblage bien précis des différents nœuds les uns avec les autres. La longueur des arcs et la manière de disposer les nœuds sur papier pour les représenter n’affichent aucune importance. Aussi, les deux réseaux ci-dessous ne présentent aucune différence topologique (Figure 10).
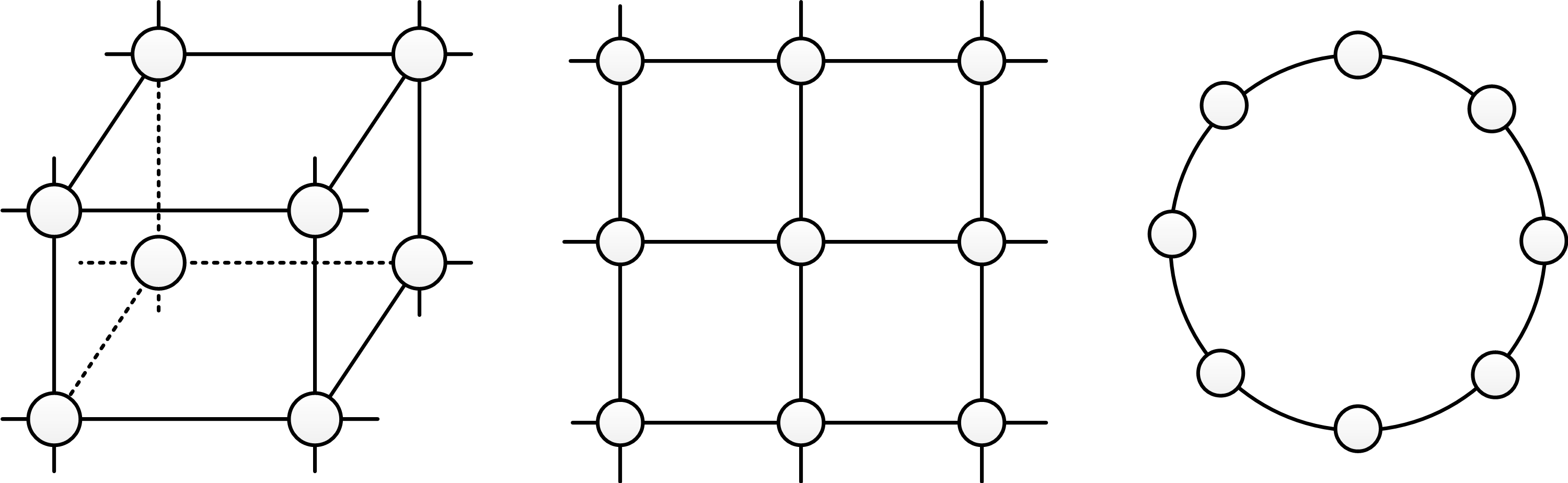
Décrire l’espace par un graphe offre de multiples avantages: en plus d’éviter tout recours à l’infini inhérent aux systèmes continus, la géométrie même de l’espace s’articulera différemment selon la façon dont auront été interconnectés les nœuds. Tout peut se concevoir; par exemple, l’image de la Figure 11 représente trois topologies régulières totalement dissemblables, bien que constituées des mêmes nœuds. À gauche, les unités d’espace sont connectées de manière à créer une grille régulière à trois dimensions. Le graphe central présente quant à lui la topologie d’une grille régulière à deux dimensions. Le dernier dessin met finalement en place un espace unidimensionnel replié sur lui-même.
Un graphe a ainsi la capacité de représenter n’importe quelle topologie, des plus régulières aux plus irrégulières, comprenant un nombre quelconque de dimensions. Tout comme pour un liquide, sa nature discrète peut passer largement inaperçue si elle est observée de loin. Une telle représentation n’arbore alors aucune incompatibilité avec la notion d’espace homogène et continu que nous avons l’habitude de côtoyer. Par contre, elle octroie de donner du sens à la nature de l’espace, tout en permettant d’expliquer des phénomènes en apparence inconcevables comme l’intrication quantique.
Plus jeune, je me souviens avoir eu beaucoup de mal à m’imprégner de l’idée que la notion d’espace puisse jaillir d’une structure exempte de ce concept. Cela nécessite d’admettre que l’espace ne dispose d’aucune réalité intrinsèque, mais émerge plutôt de propriétés plus fondamentales. J’avais pu lire qu’aux premiers instants du Big Bang, il était supposé que les notions d’espace et de temps n’existaient pas encore. Cette simple idée me retournait tout bonnement le cerveau, car je ne voyais absolument pas comment un tel prodige pouvait se produire.
Conceptualiser l’espace comme un graphe permet heureusement de se donner une bonne image mentale du processus qui pourrait sous-tendre une particularité aussi remarquable. Imaginez l’univers constitué d’une myriade d’unités d’espace fondamentales pouvant se connecter en réseau, comme expliqué plus haut. Supposez maintenant que le premier instant de l’univers corresponde à un réseau où absolument tous les nœuds sont connectés à tous leurs homologues, comme sur le dessin qui suit à gauche (Figure 12). Il va sans dire que la notion « d’espace » n’existe pas dans un tel graphe. Comme n’importe quel point peut être atteint depuis n’importe quel autre point, il n’y a aucune notion de distance qui tienne. Tout l’univers est rassemblé en une unique singularité extrêmement dense. Nous pouvons ensuite imaginer que les lois à l’œuvre dans le réseau de l’univers auraient pour conséquence de décimer la majorité des connexions. De cette manière, une notion de localité pourrait émerger petit à petit de l’ensemble, comme sur le dessin de droite. Ce processus correspondrait à l’expansion de l’univers, ayant pour effet d’augmenter la distance entre les différents points de l’espace. Cette notion de distance coïnciderait alors avec le nombre moyen de sauts requis pour aller d’un endroit à l’autre du réseau. Au plus ce nombre deviendrait-il grand, au plus l’espace semblerait se dilater.
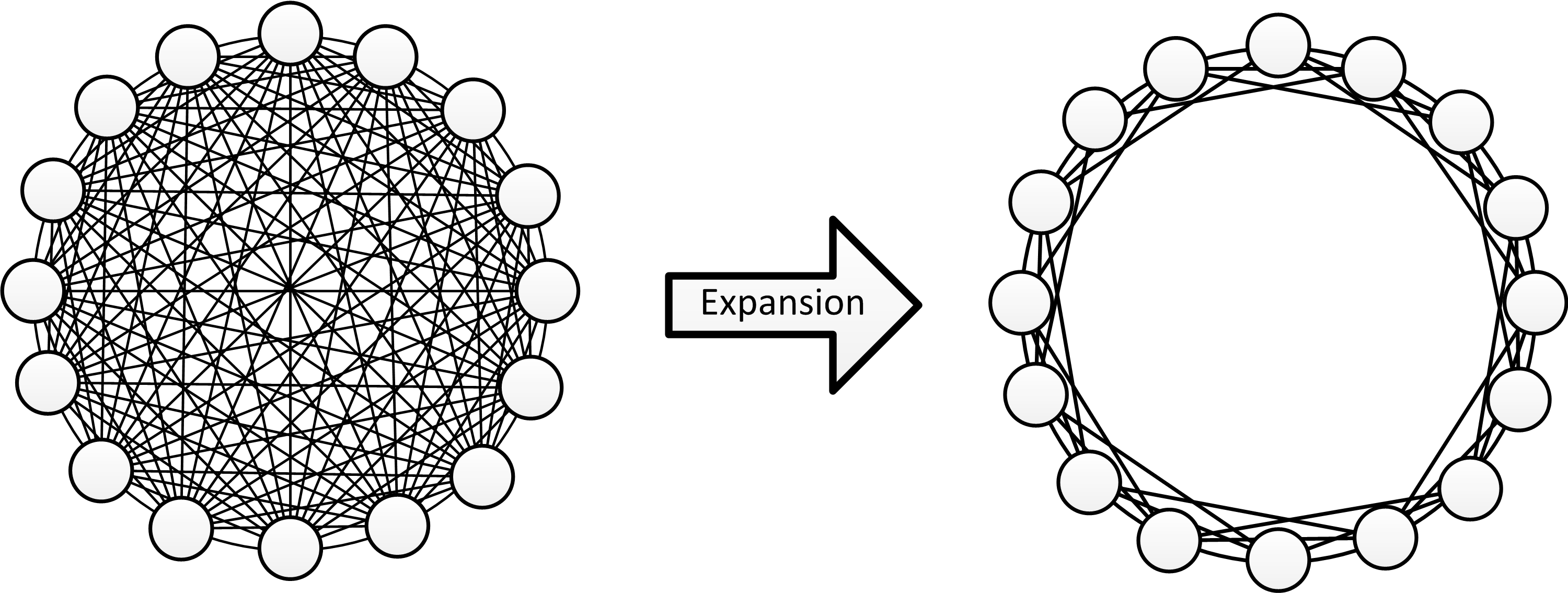
Figure 12: Illustration d’une singularité, à gauche, et du même réseau d’où a émergé une notion de localité, à droite.
Ce à quoi ressemblerait l’intrication quantique se conçoit également aisément avec un tel réseau. Imaginons un univers en deux dimensions, tel que celui illustré par le graphe de la Figure 13. Plaçons-y aussi deux particules intriquées, représentées par les boules bleues et jaunes. La topologie du réseau impose une notion de distance entre ces deux particules, constituée par le plus petit nombre de sauts qu’il faut effectuer pour se déplacer de l’une à l’autre. Ce plus court chemin est mis en évidence dans le dessin par les nœuds et liens colorés en vert. La distance « normale », telle que vue par un observateur de ces particules, correspond à cinq sauts. Rien n’empêche cependant ces deux particules de se trouver à un seul pas causal l’une de l’autre en imaginant un arc joignant directement le point de départ au point d’arrivée. Ce lien pourrait être créé lors du processus qui donne naissance à deux particules intriquées, lorsqu’elles vivent alors encore côte à côte. C’est ce lien qui leur permettrait ensuite d’apparaître comme une unique et même entité et dont les parties pourraient communiquer instantanément l’une avec l’autre. Mais pour l’observateur extérieur obligé d’emprunter le chemin en vert, cette communication directe semblerait violer le principe stipulant qu’un signal ne peut pas voyager plus vite que la lumière, c’est-à-dire d’un saut à la fois dans le réseau.
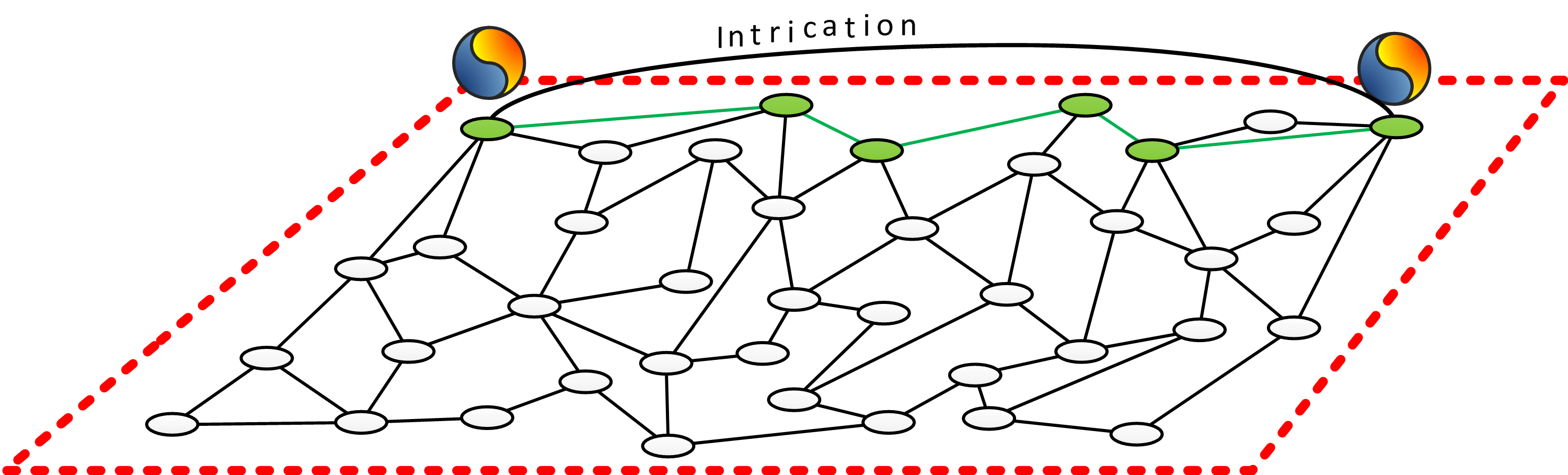
Figure 13: Illustration mettant en évidence comment l’intrication pourrait s’exprimer au sein d’un univers résultant d’un réseau à son niveau élémentaire.
L’intrication a longtemps été vue comme un concept non naturel défiant l’imagination, mais cette difficulté d’appréhension ne survient que par l’emploi du mauvais modèle pour se le représenter. Oui, l’intrication ne s’explique pas avec une vision continue et homogène de l’espace, mais cet échec souligne seulement l’inadéquation du modèle. L’histoire des sciences est jalonnée de problèmes similaires qui nous ont obligés à reconsidérer nos théories à cause d’observations de phénomènes défiant tout principe connu. Dans le modèle géocentrique d’Aristote, le mouvement temporairement rétrograde des planètes ne pouvait s’expliquer qu’en échafaudant une structure complexe de plus d’une cinquantaine de sphères tournant les unes autour des autres. La majorité de ces sphères ne correspondaient à rien d’existant, leur présence étant uniquement requise pour qu’un astre puisse circuler autour et ainsi en justifier le mouvement complexe apparent. Les trajectoires des planètes s’expliquent toutefois bien plus simplement en changeant de point de vue et en adoptant le modèle héliocentrique. Il en va de même avec l’intrication qui se conçoit beaucoup plus aisément en abandonnant la vision continue de l’espace. Peut-être tout se réduit-il au concept d’intrication et que la notion d’espace en émerge naturellement quand elle adopte un caractère homogène faisant apparaître une notion de localité dans la toile de l’univers.
À la recherche de Chronos
S’il y a bien un être mythique et insaisissable qui rit impunément au nez et à la barbe de tous, c’est bien le temps. Personne, pas même les scientifiques, ne peut définir ce qu’il est vraiment. Aussi continuons-nous à lui courir après avec l’espoir futile de l’attraper un jour, alors qu’en définitive c’est lui qui se joue de nous. Le temps a d’ailleurs ceci de particulier que nous pensons tous le connaître, en raison de l’expérience intime que nous partageons avec lui au quotidien, sans qu’il soit réellement possible de mettre le doigt dessus. Car si ce concept semble naturel, tenter de le définir est une gageure.
Beaucoup de définitions du temps ont bien été proposées au cours de l’histoire, mais comme le fait très justement remarquer le physicien Etienne Klein, chacune d’elle se réduit à une tautologie. Chacune d’elles présuppose la notion de temps pour mieux le définir ensuite. Elles rebouclent alors toutes sur elles-mêmes et aucune n’apporte d’information concrète. Pour reprendre l’un de ses exemples, la définition du temps par « milieu infini dans lequel se succèdent les événements » fait appel implicitement à la notion de temps, celui-ci devenant nécessaire pour que des événements puissent effectivement se succéder.
Si ces définitions s’affichent finalement comme de belles métaphores, les pièges du langage ne font qu’accroître la difficulté de définir ce qu’est le temps, si tant est que cela soit possible. Par exemple, une phrase banale du style « le temps passe vite » laisse sous-entendre que le temps jouit des propriétés de phénomènes qui se passent dans le temps. Mais rien n’est moins vrai, car même si tout le monde comprend ce que cette phrase suggère, il est important de noter que le temps ne peut pas être doté d’une « vitesse ». Une vitesse correspond à un rapport entre un déplacement et une durée et ne peut être définie que si le temps existe préalablement. Aussi est-il essentiel de ne pas confondre l’objet et sa fonction : le temps ne passe pas, mais il a pour fonction de faire passer les choses.
L’homme a depuis toujours ressenti le besoin de mesurer l’écoulement du temps et la sophistication des processus employés pour y arriver n’a fait que croître. Si nous nous contentions de l’observation des cycles du jour et de la nuit à l’aube de l’humanité, nous mesurons maintenant le temps avec des horloges atomiques d’une extrême précision. Le dernier record en date est détenu par une horloge qui ne dérive d’une seconde qu’en quinze milliards d’années, soit plus que l’âge de l’univers. Mais si nous pouvons mesurer le temps, nous ne pouvons pas nous en détacher. Nous subissons inexorablement son implacable emprise, ce qui nous empêche de pouvoir étudier le temps à distance comme nous pourrions procéder avec n’importe quel autre processus physique. Nous sommes irrémédiablement prisonniers du présent, pleurant un passé perdu à jamais et appréhendant un futur nous déboulant droit dessus. L’une des nombreuses questions que nous pouvons d’ailleurs nous poser sur le temps consiste à se demander si le futur existe déjà. Patiente-t-il là préalablement, attendant d’être découvert ? Ou est-ce que l’instant présent permet encore de négocier les termes de ce même futur ?
L’étude du temps qui passe a également engendré l’effet pernicieux de le fractionner en autant de sous-concepts qu’il n’y a de disciplines qui s’intéressent à lui. Une première fracture survient tout d’abord de l’incompatibilité entre le temps physique, qui existe indépendamment de nous, et le temps psychologique qui traduit l’expérience que nous en avons au niveau de notre conscience. Si le premier peut se mesurer et semble s’écouler uniformément, le second se révèle à géométrie variable et dépend de chaque individu. Deux personnes distinctes compteront toujours le temps qui passe de manière différente, en fonction de divers critères comme l’âge, la fatigue ou l’intensité des événements qu’ils perçoivent.
Cet éclatement continue toutefois pour le temps physique lui-même, avec la distinction de plusieurs flèches du temps. Le mot « flèche » traduit l’idée que, même si les équations physiques affichent une symétrique au niveau de leur paramètre temporel t, toutes sortes de phénomènes semblent ne pouvoir se mesurer que dans un seul sens, du passé vers le futur. Ces flèches surgissent dans différents domaines, comme en cosmologie, en thermodynamique, en relativité ou en physique quantique.
La flèche du temps thermodynamique exprime que l’entropie dans un système fermé ne peut que croître, c’est-à-dire qu’un système ne peut que devenir de plus en plus désordonné. Cette flèche trouverait son explication au niveau du chaos engendré par les systèmes complexes disposant de beaucoup de degrés de liberté. Même si les équations physiques à l’échelle microscopique semblent réversibles, l’évolution statistique d’un grand nombre de particules ne peut que progresser vers son état macroscopique le plus probable. Cet état est tout simplement celui pour lequel il existe le plus grand nombre de configurations microscopiques correspondantes. Imaginez par exemple un verre contenant deux couches de sable coloré parfaitement superposées. Vous pourriez les mélanger en touillant le tout d’un coup de cuillère vers la droite, mais il serait alors très improbable de retrouver le bel arrangement initial en touillant ensuite la cuillère d’un coup vers la gauche. Le problème se révèle en outre plus profond que ne le laisse penser ce point de vue purement statistique, car même la réversibilité des équations physiques à l’échelle microscopique demeure un élément controversé.
La flèche du temps cosmologique s’intéresse à l’histoire de l’univers, à son début et son avenir. Elle découle de l’apparente expansion du monde, et tente d’en extrapoler son origine et son devenir sur base de modèles tels que celui du Big Bang. Le temps de la cosmologie, universel, correspond à celui d’un observateur au repos par rapport à la distribution moyenne de la matière dans l’univers. Il n’est par contre pas possible d’extrapoler indéfiniment le temps cosmologique vers le passé, car le Big Bang constitue une limite infranchissable près de laquelle la notion même de temps perd son sens. Du coup, imaginer le début de l’histoire de l’univers nous dépasse complètement. Une telle question revient à se demander si le Big Bang a éclos dans un méta-temps lui préexistant, sorte de prélude temporel, ou si le temps et l’univers sont apparus conjointement.
Le temps de la physique quantique s’identifie à celui proposé par Newton, c’est-à-dire qu’il dispose d’un caractère universel et absolu, et qu’il s’écoule du passé vers le futur indépendamment de toute chose. Pour les ingénieurs, ce temps se traduit laconiquement par le paramètre t balisant des trajectoires temporelles le long d’un axe infini dans les deux directions. Tout comme pour les équations newtoniennes, les équations de la physique quantique, complètement réversibles, font apparaître le paramètre temps de façon explicite. Le fait que les lois physiques puissent être inversées a toujours été quelque peu ressenti comme une incohérence, car énormément de phénomènes dans la vie de tous les jours semblent impossibles à jouer à l’envers. Ainsi un verre brisé ne se reconstitue-t-il pas pour jaillir vers la main qui l’a renversé. Mais contrairement aux équations de Newton, les lois quantiques exposent une certaine forme d’irréversibilité. Celle-ci se traduit par la description des objets en termes de fonctions d’onde de probabilité, alors que ces dernières peuvent s’annuler partiellement lorsque des mesures sont réalisées sur les particules qu’elles sous-tendent. La réduction de la fonction d’onde qui résulte d’une mesure marque alors un système de façon indélébile et irréversible.
Sans conteste, c’est le temps dépeint par la théorie de la relativité d’Einstein qui heurte le plus notre sens commun. En fait, ce qu’a proposé Einstein n’est rien d’autre qu’une destitution en bonne et due forme de son statut de souverain et d’universel. Cette chute, brutale, engendra beaucoup d’émoi. Il est en effet difficile d’imaginer un espace et un temps empreint d’autre chose que de ce que nous en ressentons. D’après cette théorie pourtant, temps et espace s’afficheraient comme deux aspects émanant d’une même structure, absolue, que l’on nomme espace-temps. Aussi la perception de l’espace et du temps devient-elle fonction de la trajectoire qu’effectue un observateur dans l’univers. Cette conception a pour conséquence directe que deux entités manifestant une vitesse relative l’une par rapport à l’autre ne voient pas l’univers de la même façon et ne ressentent pas l’écoulement du temps de manière identique. Vu de cette façon, le temps perd son statut de force externe séquençant le déroulement de l’univers, mais devient directement dépendant de la dynamique de ces événements. L’espace-temps constituerait quant à lui une entité figée et complètement hors du temps.
Le postulat que des observateurs différents ne ressentent pas l’écoulement du temps de manière identique implique que leur horloge ne batte pas au même rythme et que la notion de simultanéité perde son sens. Il devient alors impossible de dire : « nous sommes maintenant » sans que ce « maintenant » ne se trouve dans le futur ou le passé d’un autre observateur. Malgré ces différences de point de vue, il faut tout de même noter que l’espace-temps respecte toujours le principe de causalité; ainsi, si un événement A peut influer sur le cours d’un événement B, alors A se manifestera toujours antérieurement à B, qu’importe l’observateur considéré. C’est de cette manière que se manifeste la flèche du temps en relativité.
Einstein ne s’est pas arrêté en si bon chemin et a proposé un peu plus tard un modèle plus complet qui explique également l’origine de la gravitation. Selon ce modèle, celle-ci ne serait pas une force à part entière comme le sont les autres forces de l’univers (électromagnétisme, etc.), mais résulterait plutôt d’une déformation géométrique de l’espace-temps autour de la matière. La matière et l’espace-temps mèneraient alors une danse complexe. Au cours de celle-ci, la première déformerait la seconde, influant sur la dynamique temporelle et sur les trajectoires des objets se mouvant dans l’univers. En retour, les déplacements de masse en résultant déformeraient l’espace-temps de plus belle. Ce n’est donc plus seulement la vitesse relative des observateurs qui impacterait la vitesse d’écoulement du temps, mais aussi la distribution des masses en présence. L’une des conséquences de cette théorie implique qu’une personne vivant en montage doit vieillir imperceptiblement plus vite qu’un individu habitant à la mer, à cause de la légère différence de gravité qu’ils y subissent. Aussi saugrenue qu’une telle implication puisse paraître, ces effets ont bel et bien été vérifiés expérimentalement.
Comme nous pouvons le voir, la notion du temps qui passe est encore loin d’être unifiée en un concept théorique unique. L’incompatibilité est flagrante entre les deux théories phares de la physique moderne que constituent la relativité et la mécanique quantique. Leur différence de vision pose beaucoup de problèmes, car ces deux conceptions, inattaquables dans leur domaine respectif, nous imposent de nous résoudre à l’idée que les différentes approches du temps doivent correspondre en fin de compte aux multiples approximations d’un concept plus fondamental.
Construction d’une prison sans roulettes
Quand j’ai découvert pour la première fois des articles de vulgarisation sur la théorie de la relativité, j’ai tout d’abord pensé que les choses étaient encore plus compliquées que je ne l’imaginais. Nous avons une telle intuition du temps qu’il nous est extrêmement difficile de nous défaire de l’image que nous nous en forgeons depuis notre plus jeune âge ; celle d’une flèche unique qui cadence le déroulement du monde. Se figurer que le temps perd son sens aux premiers instants du Big Bang, qu’il n’existe pas avant celui-ci ou que des personnes peuvent vieillir plus ou moins vite en fonction de leur mouvement dans l’espace est plus que déroutant. Pourtant, les preuves ne manquent pas, puisque cette théorie a été maintes fois testée en employant des horloges atomiques extrêmement précises pour éprouver tous ces phénomènes. À l’époque, j’ai admis la chose, faute de l’avoir réellement comprise.
Plus tard, j’ai bien sûr eu l’occasion de me plonger dans des livres présentant la relativité avec beaucoup plus de détails — il faut entendre par là : avec beaucoup plus de calculs —. J’ai assimilé les équations, résolus mes petits exercices, mais fondamentalement, je ne comprenais toujours pas. Il me manquait perpétuellement un petit quelque chose pour être intimement convaincu de la logique qui se cachait derrière toute cette théorie. J’ai fini par comprendre…, et le jeu en valait certainement la chandelle, car finalement, la théorie de la relativité ne rend pas le concept de temps plus compliqué ou plus bizarre. Elle le simplifie, contre toute attente, et le revêt d’une élégance rare. La question du temps ne s’en trouve pas entièrement résolue pour autant, mais un coin du voile en est néanmoins soulevé.
Peut-être vous demandez-vous pourquoi je tiens à ce point à parler du temps. La réponse provient des conclusions qu’il est possible d’en tirer et qui concordent parfaitement avec les déductions qui ont été échafaudées plus haut sur la nature de la conscience. En effet, la relativité ne dit pas particulièrement que le temps s’expérimente différemment pour des observateurs distincts en mouvement dans l’univers, ce qu’elle dit en filigrane est plutôt que le temps n’existe pas; il s’agit d’un épiphénomène qui ne prend forme qu’au niveau de notre conscience.
Je vais repartir des automates cellulaires qui ont été présentés précédemment pour expliquer la possibilité de cette mise en perspective. Ces consttructions ont encore une fois juste valeur d’exemple pour illustrer certains principes qui pourraient façonner l’univers. Comme ce dernier semble enraciné dans le paradigme quantique, une structure de même nature serait plus appropriée pour le décrire que de simples cellules binaires [27]C’est d’ailleurs ce à quoi s’emploie la théorie de la gravitation quantique à boucles. Celle-ci ne présuppose aucune structure d’espace-temps absolue préexistante, mais modélise l’univers par l’évolution d’un graphe quantique, ou mousse de spin, dans lequel chaque nœud représente un quanta d’espace. . Un automate cellulaire offre cependant l’avantage de ne pas noyer le message dans des complications qui feraient perdre de vue l’essentiel : la causalité.
Comme nous l’avons vu auparavant, la construction d’un tel automate repose sur une simple règle de causalité. En d’autres termes, chaque cellule d’une rangée est façonnée sur base du contenu des cellules avoisinantes dans la rangée précédente. Il n’y a pas de temps à proprement parler au sein de la grille qui résulte de ce processus, hormis celui nécessaire au calcul de son contenu. Aussi n’y a-t-il pas d’ordre de construction imposé pour l’élaboration de la grille complète tant que la causalité est respectée. Par exemple, les deux grilles de droite de la Figure 14 forment des édifications partielles totalement valables qui mèneront au même résultat, représenté par la grille de gauche. Leur création s’apparente à la construction d’un mur de briques. Vous pouvez les monter dans l’ordre que vous voulez tant qu’une brique repose complètement sur d’autres briques du dessous. Cette flexibilité s’oppose à la conception linéaire du temps que nous entretenons habituellement. Il n’est pas possible ici d’attribuer un numéro de séquence à chaque cellule, pour déterminer un ordre strict de calcul, sans que cet ordonnancement paraisse complètement arbitraire.
Le fait que la règle de causalité dépende localement de la rangée précédente impose une vitesse de déplacement limite de l’information dans la grille. Elle se traduit ici par l’interdiction qu’une case noire puisse se décaler de plus d’un pas vers la gauche ou vers la droite à chaque nouvelle rangée. Aussi est-il nécessaire de construire au minimum n rangées pour que le contenu d’une cellule puisse influencer celui d’une colonne se trouvant à une distance de n pas. L’illustration ci-dessous est basée sur la règle 110 et met en évidence cette vitesse limite de déplacement de l’information dans la grille (Figure 15). Cette restriction pourrait s’appeler la vitesse de causalité.
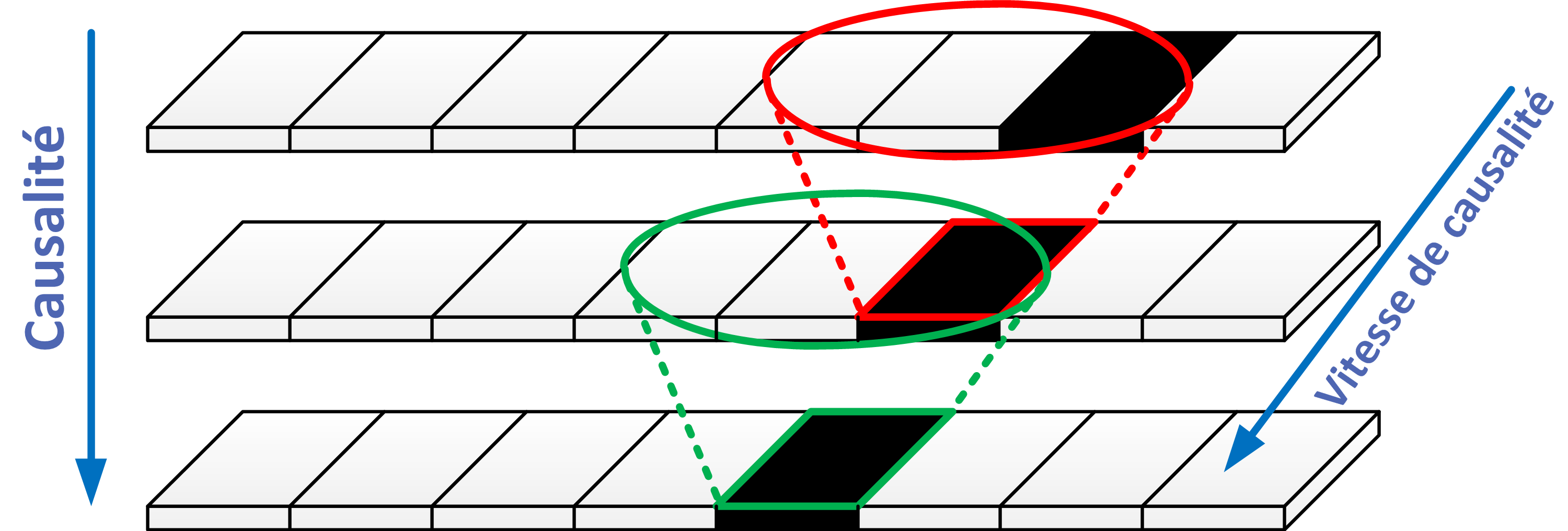
Figure 15: Illustration de la vitesse de causalité au travers des trames successives d’un automate cellulaire.
Le terme « vitesse » employé ici est quelque peu usurpé, car il ne s’agit pas d’une vitesse usuelle. Une vitesse est en effet définie comme une différence de distance par rapport à un incrément de temps, mais encore une fois, le résultat engendré par un tel automate cellulaire se résume juste à une grille. Elle ne contient aucune notion de distance ou de temps, il s’agit d’un objet complètement statique. Vu que la verticalité ou l’horizontalité ne représentent rien en soi, la vitesse de causalité n’arbore aucune dimension. Pourtant, si je vous demandais de placer les axes correspondants sur cette grille, j’ai la certitude que vous dirigeriez l’axe du temps verticalement vers le bas et l’axe d’espace perpendiculairement à celui-ci. C’est en effet de cette façon que nous lisons intuitivement la grille une fois que nous savons comment elle est construite ; c’est-à-dire que chaque tranche horizontale est vue comme une tranche d’espace unidimensionnelle, tandis que toutes les couches successives semblent représenter l’évolution de cet espace au fil du « temps ».
Il s’avère que cette vision intuitive de l’interprétation du temps et de l’espace dans cette grille n’est pas complètement fausse. La réponse exacte s’avère toutefois un peu plus complexe et la raison provient de notre point de vue extérieur à la grille, nous ne l’interprétons pas depuis l’intérieur. Mais comme nous l’avons vu plus haut, cette grille est figée et la séquence permettant de la calculer se montre partiellement arbitraire. Aussi pour discerner le temps nous faut-il plonger au sein de celle-ci pour tenter d’y déceler du mouvement. Le mouvement entretient une relation privilégiée avec le temps, il n’est ainsi pas possible de définir l’un sans l’autre. Essayons donc de nous imaginer comme une entité immergée dans la grille de l’automate cellulaire. Nous ne pourrions y persister en son sein que s’il existe un lien de causalité pour maintenir l’intégrité de notre entité d’un pas causal à l’autre, afin de subsister. De ce point de vue, comment s’écoulerait le temps et comment percevrions-nous l’espace ?
En fait, tout dépend du mouvement. Commençons par le cas le plus simple où l’entité évolue verticalement d’un pas à l’autre (Figure 16). Les déplacements successifs de cette entité sont représentés par les cases colorées en bleu dans la grille. Chaque case correspond à l’état de cette entité à un « instant » donné. Aussi sa ligne de vie se traduit-elle par la colonne bleue verticale filant vers le bas. Si la causalité se limite à cloner l’entité d’une rangée à la suivante à chaque pas, celle-ci ne doit ressentir aucun effet particulier. Il est donc naturel que, pour elle, l’axe du temps se superpose à sa ligne de vie, c’est-à-dire à l’axe vertical de la figure.
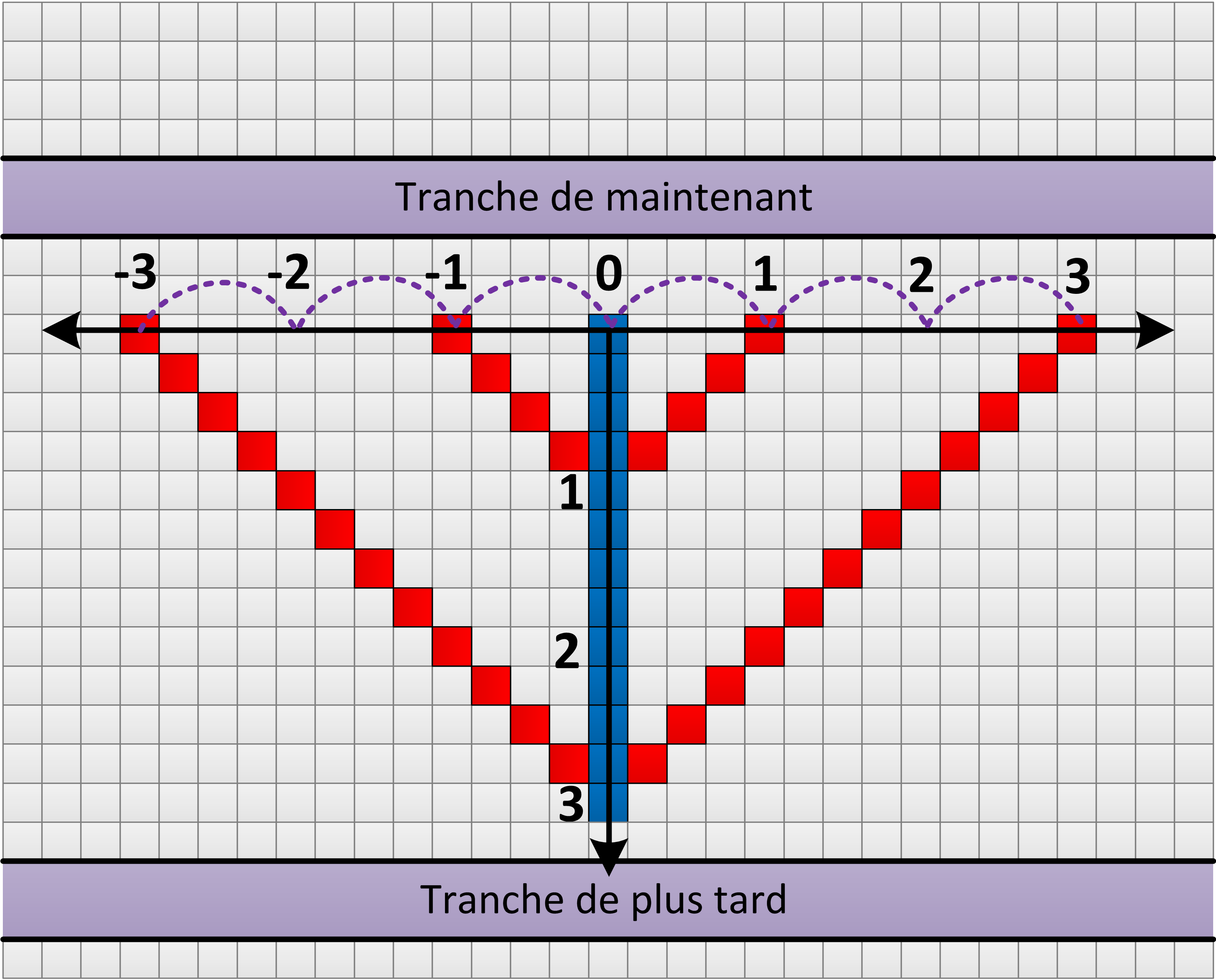
Figure 16: Construction des axes d’espace et de temps, relatifs à une entité évoluant selon un axe vertical.
Intéressons-nous maintenant à sa perception de l’espace. Pour l’entité, à un instant donné, l’espace correspond à l’ensemble des autres cases de l’automate qui lui semblent exister simultanément. La notion de distance qui accompagne le concept d’espace implique que nous pouvons identifier ces cases sur base du temps nécessaire pour y accéder à une vitesse donnée. Par exemple, une case située à une distance triple d’une autre doit requérir trois fois plus de temps pour être atteinte en se déplaçant à vitesse égale. Le dessin de la figure illustre ce concept en imaginant quatre projectiles lancés simultanément de la gauche et de la droite de l’entité à l’instant zéro. Deux des projectiles sont placés à une distance unitaire arbitraire de l’entité, tandis que les deux autres sont disposés au triple de cette distance. L’évolution de ces projectiles est représentée par les cases colorées en rouge. Ils voyagent tous à la vitesse causale, si bien que pour que la notion de temps et d’espace se révèle cohérente, il est nécessaire que les paires de projectiles situés à même distance arrivent simultanément sur l’entité. Il faut de plus que ce temps croisse proportionnellement à la distance perçue. La seule manière de respecter ces conditions consiste à placer l’axe d’espace horizontalement sur la figure, et c’est alors de cette façon que celui-ci prend son sens pour l’entité évoluant au sein de l’automate. Cette vision des choses correspond parfaitement avec l’intuition que nous pouvons en avoir de prime abord.
La situation s’avère toutefois un peu différente si l’entité se déplace latéralement au sein de la grille. L’exemple de la Figure 17 considère son cheminement à la moitié de la vitesse causale, ce qui se traduit par une règle d’évolution lui imposant un pas de côté lors d’un déplacement sur deux. Si cet écart ne modifie pas la nature de l’entité, il est logique que celle-ci ne perçoive pas sa propre vitesse de déplacement, lui laissant une impression de repos au sein de l’espace. Aussi, tout comme dans l’exemple précédent, sa perception du temps qui passe doit correspondre à sa ligne de vie et l’axe du temps aligné comme tel. Ce dernier perd alors sa verticalité pour s’incliner et coller à la trajectoire de l’entité.
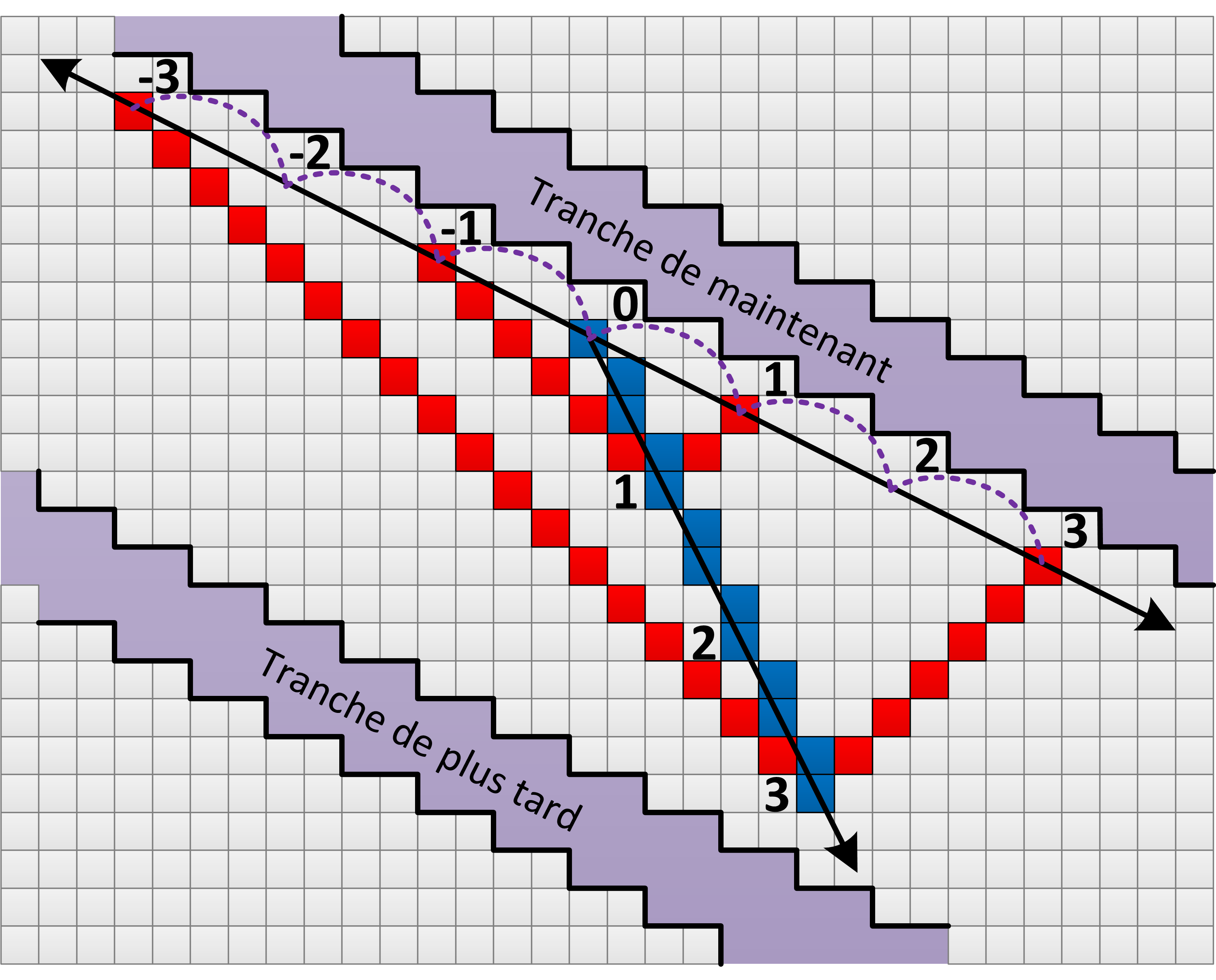
Figure 17: Construction des axes d’espace et de temps pour une entité évoluant selon un axe incliné par rapport à la verticale.
Cette modification de trajectoire a également pour conséquence de changer fondamentalement la façon dont elle va interpréter la nature de l’espace. Ce changement de perspective s’illustre en reconsidérant les quatre projectiles lancés simultanément à différentes distances, et permettant d’identifier les cases de l’automate correspondant au même « maintenant ». Pour que la notion d’espace reste cohérente, la seule manière de procéder consiste à incliner son axe d’un même angle que l’axe temporel. L’opération octroie alors aux projectiles situés à égale distance d’arriver simultanément sur leur cible, tout en voyant leurs temps de cheminement, lus sur l’axe temporel, correspondre aux distances parcourues. Le phénomène se remarque clairement sur la figure, au travers des deux paires de projectiles rouges à distance simple et triple qui atteignent l’entité bleue au même moment. Cette cohérence ne peut être atteinte en plaçant l’axe d’espace horizontalement, comme c’était le cas dans l’exemple précédent.
Cette expérience de pensée illustre parfaitement la duplicité que joue la perception de l’espace et du temps depuis l’intérieur de l’automate. En tant que tel, l’automate correspond à une vaste grille représentant une histoire complète, du début à la fin, comme un film sur DVD. Mais l’interprétation de son contenu par des entités évoluant en son sein dépend totalement de la manière dont elles persistent d’un pas causal à l’autre. Ce qui constitue purement du temps ou de l’espace pour l’une est un mélange des deux pour l’autre, et inversement. La grille complète peut être vue comme un espace-temps immuable, tandis que la dissociation de cet espace et de ce temps s’avère subjective et dépend de la lecture qui y est réalisée. En d’autres termes, il s’agit du même gâteau, mais des entités différentes ne le découperont pas en tranches de la même façon.
Cette conception rend ces notions de temps et d’espace toutes relatives, car elles n’existent pas à un niveau fondamental. Ce sont des épiphénomènes sujets à interprétation et qui surgissent d’un tout plus complexe qu’il y parait. Cette compréhension, gratifiante, explique remarquablement bien comment le temps a pu ne pas exister avant la naissance de l’univers. Elle nous permet de nous rendre compte que ce concept perd son sens aux premiers instants du monde, là où les notions d’espace et de localité n’étaient pas encore apparues. Mais comme pour tous les autres points abordés dans ce livre, il n’y a pas de réponse pleinement satisfaisante. Si l’univers s’apparente un peu à un automate cellulaire, rien n’explique dans quel méta-temps — sorte de temps hors de notre temps — il a pu être créé. Cette notion se situe au-delà de notre capacité de compréhension.
Le physicien Etienne Klein décrit métaphoriquement le temps comme semblable à une « prison à roulettes ». La prison symbolise le fait que nous y sommes piégés dans le présent, incapables de nous mouvoir librement vers le passé ou le futur. Les roulettes permettent au temps de nous pousser inéluctablement en avant, que nous le voulions ou non. Mais si le temps n’existe pas, qu’il nous illusionne, il s’en suit que cette prison constitue un pur produit de notre esprit, qu’il se construit en découpant une tranche d’espace-temps lorsqu’il essaie d’en interpréter la réalité. Cette prison n’a dès lors pas besoin de roulettes, car il ne subsiste plus rien ni personne pour la pousser en avant. Cette conclusion peut sembler surprenante, mais elle se marie merveilleusement bien avec la vision de la multiplicité temporelle de la conscience. Si celle-ci se décline en une collection d’instantanés hors du temps, telles les multiples diapositives d’un film, alors ces images peuvent s’enchâsser facilement dans l’espace-temps. Ni l’une ni l’autre ne requiert la notion de temps pour exister. À chaque instant, une conscience peut ainsi être vue comme une petite partie figée de l’espace-temps. En raison de son extrême capacité d’autoréférencement, elle est sa propre spectatrice et interprète le monde en un édifice d’unités de compréhension abstraites, émotionnelles et logiques. Mais tel un rubis sur une bague, celle-ci demeure sertie à jamais, immobile, dans l’écrin que constitue l’univers.
Ralentissement des horloges et autres bizarreries
Comprendre que la lecture de l’espace et du temps dépend de la trajectoire empruntée dans l’espace-temps est un premier pas pour appréhender les manifestations un peu étranges de la relativité. Mais il faut également bien concevoir ce que signifie « vieillir » pour saisir le phénomène de ralentissement des horloges. Le vieillissement biologique est lié au métabolisme et au cortège de divisions cellulaires qui l’accompagne. Ce processus complexe dépend à son tour des myriades de réactions chimiques qui se déroulent au sein de chaque cellule. Ces réactions sont elles-mêmes soumises aux forces électromagnétiques qui influent sur la façon dont les atomes des différentes molécules vont se lier les uns aux autres, telle une gigantesque partie de billes, version magnétique.
Une force ne peut toutefois pas agir instantanément à distance [28]D’après la théorie quantique des champs, une force est un concept qui naît de la capacité qu’ont les particules élémentaires à s’échanger de petits paquets d’énergie. Ce gain d’énergie pour l’une se réalise au détriment de l’autre et cela a pour effet de modifier la trajectoire de chacune d’elles. Mais cet échange ne se produit pas instantanément, il s’opère au travers de particules médiatrices de force que l’on appelle les bosons. Par exemple, le boson de l’électromagnétisme se révèle être le photon. Un boson est modélisé comme une perturbation se propageant au travers de ce que l’on appelle un champ quantique. : il s’agit d’une perturbation locale qui doit se propager pour atteindre les autres particules sur lesquelles elle peut agir. Sa vitesse de déplacement doit dès lors être limitée à la vitesse de la lumière ; c’est-à-dire à ce que nous pouvons appeler la vitesse de causalité. Il n’est alors pas étonnant que la vitesse de déplacement d’un objet affecte la capacité des particules qui le constituent à s’échanger ces petits paquets d’énergie, et donc la dynamique des forces en présence. Ce raisonnement, vrai pour le vieillissement d’un être vivant, l’est aussi pour n’importe quel autre processus lié au temps qui passe, telle une horloge.
La mesure du temps s’est toujours traduite par l’examen du mouvement des horloges. Un tel dispositif enferme toujours un mécanisme doté d’un engrènement périodique constant, dont chaque révolution se confond autant que possible avec la précédente. C’est de cette manière que des horloges distinctes pourront égrener le temps de manière comparable et prédictible, même si les processus physiques qui les animent diffèrent. Le terme « horloge » vous évoque peut-être la pendule de votre grand-mère. Toutefois, plus une horloge est grande, plus celle-ci subira les erreurs dues à sa précision de fabrication et à d’autres phénomènes physiques parasites. Il est alors naturel que les horloges atomiques manipulent directement la vibration d’une poignée d’atomes pour atteindre leur précision remarquable. Plus le processus physique s’avère élémentaire, plus ce processus incarnera le fidèle témoin de l’avancement temporel de l’univers.
Essayons maintenant d’imaginer une horloge élémentaire dans notre automate cellulaire, afin de constater comment le mouvement influence la façon dont elle va compter le temps qui passe. La manière dont elle en sera affectée caractérisera n’importe quel autre phénomène, car un processus physique résulte finalement du gigantesque assemblage de phénomènes élémentaires analogues. Comme le monde dépeint par nos automates se déploie en une seule dimension d’espace, cette horloge est simplement constituée de deux extrémités entre lesquelles rebondit une particule se déplaçant à la vitesse de causalité. La mesure du temps se concrétise alors aisément par le comptage du nombre d’aller-retour effectués par cette particule. Pour ceux qui connaissent, ce système s’apparente à l’horloge à photons généralement employée pour expliquer la théorie de la relativité.
Commençons par l’horloge A, à gauche dans le dessin qui suit (Figure 18). Elle est constituée de deux parois A1 et A2 au repos par rapport à notre trame de référence. Elles sont séparées par dix cellules de la grille de l’automate, si bien qu’il faut également dix pas causals à la particule rouge pour parcourir cette distance. Le retour s’effectue de manière identique et la particule revient alors à son point de départ à la vingtième rangée de l’automate. Cette horloge compte le temps avec des tic-tac, un tic survenant chaque fois que la particule atteint le côté droit de l’horloge, un tac quand elle atteint le côté gauche. Par facilité, nous pouvons considérer qu’un tic-tac, soit un aller-retour, équivaut à une seconde. Les tranches d’espace sont colorées en mauve si la particule qu’elles contiennent se déplace vers la droite, en gris sinon.
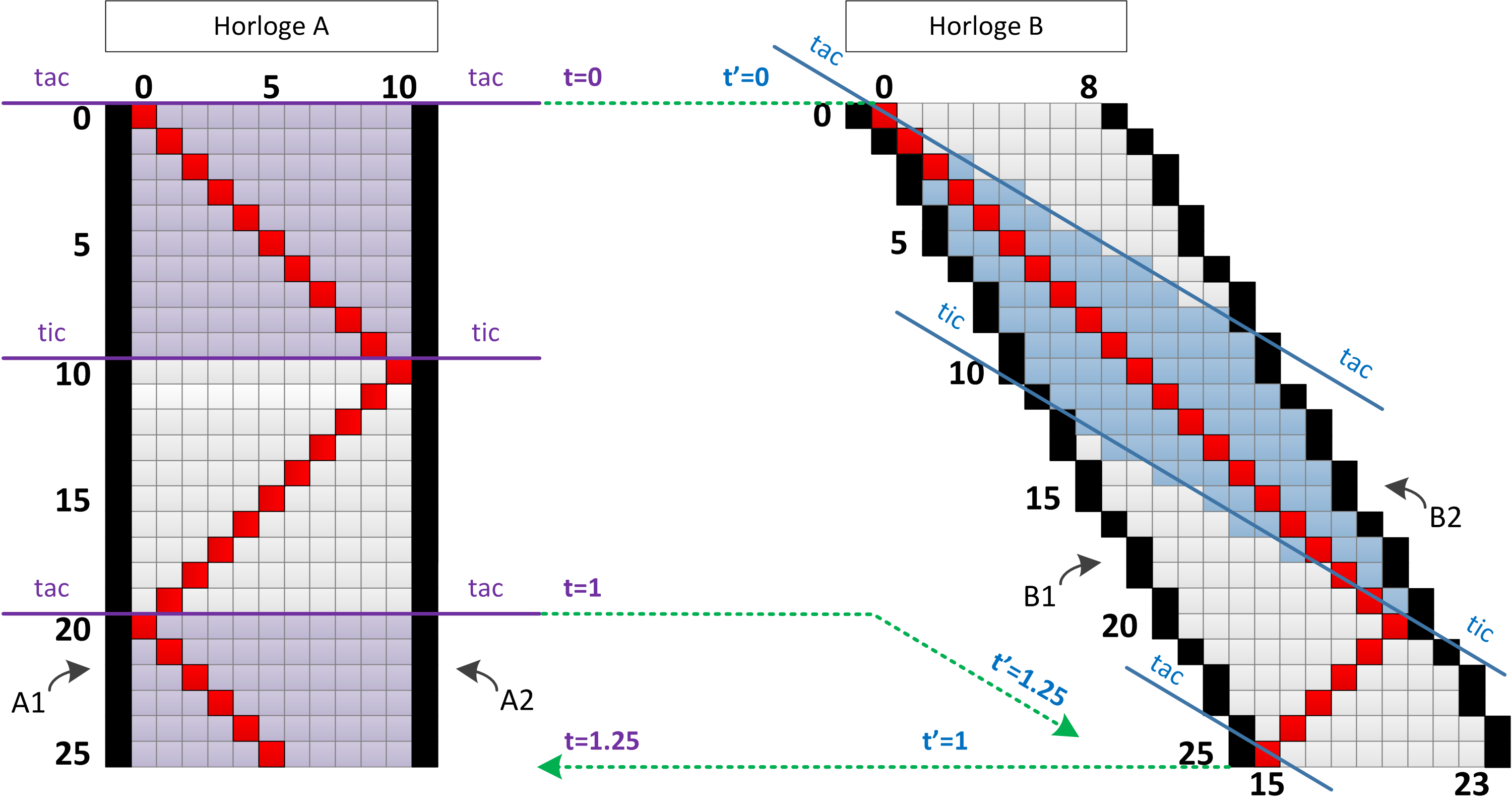
Figure 18: Visualisation de l’écoulement du temps pour deux horloges en mouvement l’une par rapport à l’autre. Du fait de la manière différente qu’elles ont de mesurer le temps et l’espace, chacune d’elle voit l’autre ralentir.
Examinons maintenant ce qu’il advient si un clone de cette horloge voyage, lui, à 60 pour cent de la vitesse de la lumière par rapport à l’originale. Cette horloge B est dépeinte à la droite de la figure. Elle est constituée des deux parois B1 et B2 affichant un angle du fait de leur vitesse de déplacement. Cette vitesse imprimée à l’horloge B a pour conséquence de distordre complètement la dynamique de son tic-tac interne. Il faut en effet vingt pas causals pour que la particule rouge puisse atteindre la paroi de droite de l’horloge, soit le double de ce qui est requis dans l’horloge A. Le retour se révèle par contre plus rapide, car la particule vient à la rencontre de la paroi ; il ne nécessite que cinq pas. Au total, il faut 25 pas causals pour battre la mesure du tic-tac de l’horloge B, là où il n’en fallait que 20 pour l’horloge A. La perception de l’horloge A se traduit alors par l’impression que son clone fonctionne moins rapidement, puisque chaque tic-tac de B correspond à 1,25 tic-tac de A. Ce qui vient d’être énoncé repose simplement sur un peu de géométrie et de comptage, il n’y a rien de saugrenu là-dedans…, du moins pas encore.
Lorsque l’on regarde les distorsions de l’horloge B, il est difficile d’imaginer qu’un astronaute voyageant lui aussi à 60 pour cent de la vitesse de la lumière ne se rende compte de rien. Par exemple, s’il disposait d’une (grosse) horloge à photon dans son vaisseau, ne pourrait-il pas voir que le fameux photon met quatre fois plus de temps pour aller d’un miroir à l’autre que pour le retour ? La réponse est non, car comme nous l’avons vu précédemment, il ne faut pas oublier que ce voyageur ne percevra pas l’espace-temps de la même façon. Pour lui, ce qu’il convient d’appeler « l’espace », à un moment donné, est incliné par rapport à l’horizontale. C’est pourquoi les lignes de tic et de tac, en bleu sur la figure, forment un angle et délimitent des losanges en lieu et place des rectangles que nous avions précédemment. En conséquence, le tic de l’horloge B découpe la ligne B1 à équidistance des deux tacs qui l’encadrent, ce qui donne la sensation à l’astronaute que le temps aller du photon correspond exactement au temps retour.
Pourrait-il se rendre compte par ailleurs d’une quelconque distorsion d’espace ou de temps ? La réponse est encore une fois non. Même s’il faut 25 pas causals à l’horloge B pour effectuer un aller-retour, soit cinq de plus qu’au repos, cette distorsion modifie la dynamique de chacune des innombrables particules constituant l’astronaute, son vaisseau spatial, son horloge à photon ou encore l’horloge de sa grand-mère qui l’accompagne à chacun de ses voyages. Toutes les durées (en matière de pas causals) sont rallongées dans les mêmes proportions et il n’aurait donc aucunement la sensation que quelque chose ait ralenti. Le raisonnement est le même pour la distorsion de l’espace. La distance séparant les deux parois de l’horloge B, mesurée le long d’une ligne de tic ou de tac, se voit couvrir 12,5 cellules de l’automate, soit un quart de plus que pour l’horloge au repos. Mais cette dilatation est dupliquée pour chacune des particules de tout cet arsenal galactique, si bien que rien ne semble changer pour les observateurs à bord.
Il est par ailleurs intéressant de constater un autre phénomène étrange prédit par la relativité, celui de la contraction des longueurs. Celle-ci s’observe en examinant la distance séparant les deux parois de l’horloge B, en se plaçant du point de vue de l’horloge A, c’est-à-dire en mesurant les longueurs le long de lignes horizontales. L’horloge B donne alors l’impression de rétrécir, ne couvrant plus que huit cellules de l’automate. Ce rétrécissement est dû au fait qu’une mesure réalisée selon une ligne horizontale, donc pour un instant bien défini dans le référentiel de l’horloge A, correspond à deux instants différents du point de vue de l’horloge B. Lorsque le tic-tac de A est à zéro, la paroi gauche de B sonne également zéro, mais sa paroi de droite, elle, se situe dans son passé. L’explication de tous ces mystères de dilatation du temps ou de contraction des longueurs découle de l’observation que ni l’horloge A ni l’horloge B ne mesure le temps et les longueurs en comptant directement les cellules de l’automate cellulaire. Elles se réfèrent plutôt à des tic-tac de processus physiques élémentaires. Une distorsion uniforme de tous ces processus a pour conséquence de ne finalement rien changer à toutes les perceptions qui en découlent. Le volume d’espace-temps dans lequel se jouent ces fameux tic-tac reste d’autre part constant, qu’importe la vitesse de déplacement de l’horloge. Cette propriété peut s’observer dans la figure au travers du losange bleu de l’horloge B qui couvre exactement la même surface que le rectangle mauve de l’horloge A. Encore une fois, l’automate de cet exemple se résume à une simple grille sans dimension, et c’est seulement l’interprétation subjective du temps et de l’espace qui change en fonction du point de vue.
Nous nous sommes jusqu’à présent limités à observer l’horloge B du point de vue de l’horloge A. Ce regard laisse peut-être à penser que cette dernière jouit d’un statut particulier. Après tout, parmi toutes les vitesses possibles de déplacement, celle demeurant immobile par rapport à la trame de l’automate cellulaire ne devrait-elle pas sonner plus « juste » que les autres ? Il est très intéressant d’examiner l’autre point de vue pour répondre à cette question ; c’est dire de regarder la mesure du temps de l’horloge A, tout en étant accroché au référentiel de B. Pour ce faire, imaginons que les deux horloges se synchronisent tout en haut de l’automate en marquant le temps zéro au niveau de la première rangée de cellules. Cette synchronisation est soulignée par la ligne pointillée verte, en haut du dessin. Nous avions déjà vu que lorsque l’horloge B finit d’égrener un tic-tac, l’horloge A compte 1,25 mesure de son côté, comme le souligne la ligne verte tout en dessous. Mais il s’avère plus surprenant de regarder combien de temps s’est écoulé pour l’horloge B une fois que A a fini de battre exactement une mesure. La projection de cet événement doit être effectuée selon un axe d’espace incliné, parallèle aux lignes de tic-tac de l’horloge B. Elle est illustrée par la ligne verte du milieu sur le dessin. Comme nous pouvons le voir, l’intersection de cette ligne avec l’axe temporel de l’horloge B a lieu lorsque cette dernière marque exactement 1,25 mesure. Ce chronométrage signifie que, du point de vue de B, c’est l’horloge A qui ralentit et compte le temps moins vite. Il existe en pratique une symétrie parfaite entre le point de vue de l’une et de l’autre. Chacune à la sensation de ne pas se mouvoir dans l’espace et que c’est l’autre horloge qui file à toute vitesse. Chacune voit l’autre horloge rétrécir et chacune perçoit le ralentissement du battement de sa jumelle.
Ce phénomène de double ralentissement du temps qui semble si paradoxal n’est finalement dû qu’à une facétie géométrique. Pour s’en convaincre, il peut aider de redessiner le même diagramme que précédemment, mais en prenant soin de redresser les axes de temps et d’espace de l’horloge B de façon à ce que ceux-ci apparaissent orthogonaux. Ce recadrage a pour conséquence directe de déformer les axes de l’horloge A et le résultat de cette manipulation est illustré sur le dessin qui suit (Figure 19).

Figure 19: Visualisation de l’écoulement du temps pour deux horloges en mouvement l’une par rapport à l’autre, en orientant les axes de la trame de manière à ce que l’horloge B semble évoluer verticalement.
Comme nous pouvons le constater, le simple fait de redessiner la même figure un peu différemment, tout en conservant les relations de causalité entre les cellules, donne maintenant l’impression que c’est l’horloge B qui sonne le temps juste. Son temps de parcours semble symétrique entre l’aller et le retour, tandis que ce n’est plus le cas pour l’horloge A. Les deux diagrammes sont pourtant parfaitement identiques et décrivent la même dynamique et les mêmes relations. Les liens de causalité suivent le même chemin, seul change la géométrie avec laquelle est schématisée chaque cellule élémentaire de l’automate. Mais la forme des cellules ne signifie rien en soi, il ne s’agit que d’un artifice nécessaire à leur représentation. L’unique élément qui compte vraiment se réduit au lien causal qu’entretiennent les cellules les unes avec les autres, et qui lui n’a pas changé.
Tous les mouvements effectués à vitesse constante dans l’espace-temps semblent tous équivalents. Il est impossible de déclarer l’un plus « juste » que l’autre, car ils constituent tous autant de points de vue arbitraires parfaitement valables. En d’autres termes, si l’univers embarque un mécanisme semblable à notre automate cellulaire, dans le sens où il disposerait d’une trame causale de cellules en filigrane, cette trame pourrait bien s’échapper de la portée de tous nos instruments de mesure. Un instrument doit en effet se baser sur un quelconque processus physique pour obtenir un résultat, mais il se trouve que tous ces processus s’inscrivent dans cette même trame et subissent en conséquence des déformations identiques. Il n’est donc probablement pas possible de constater ces déformations en les comparant à une référence fixe, car cette opération ne pourrait réellement se réaliser qu’en observant l’univers depuis l’extérieur.
Cette petite dissertation sur la dynamique de l’univers doit nous faire comprendre que le moteur qui le fait évoluer n’est pas le temps, il s’agit de la causalité [29]Nous parlons ici de causalité non classique, hors de l’espace et du temps, mais qui peut engendrer des événements se trouvant, eux, dans la lecture que nous en avons. et du changement qu’elle engendre. Mais celle-ci ne revêt aucun aspect linéaire qui permettrait d’ordonner les événements du monde sur une grande ligne temporelle. Elle tisse plutôt une toile dense de fils s’enchevêtrant inextricablement les uns dans les autres pour produire le motif complexe de l’espace-temps que nous connaissons et le cortège d’événements qui le font évoluer. Chaque fil correspond à la ligne de vie d’une particule et ceux-ci s’entrecroisent en mailles élaborées lors de chaque interaction qui jalonne leur existence. Mais le temps, lui, est le produit de la conscience. C’est la perception que se construit le cerveau en glissant le long de toute une tresse d’univers. De cette sensation découle l’image que nous nous imaginons du temps, celle d’un fleuve dévoilant inexorablement les événements les uns après les autres le long de son lit. Et tout comme la tresse concède une certaine épaisseur, l’instant présent n’arbore pas une durée nulle comme le conceptualisent les physiciens. Notre conscience, à un instant, est construite sur la rémanence du passé et sur l’anticipation de l’avenir. Elle se voit enrobée de strates successives d’événements ayant eu lieu, ainsi que de ceux que nous voyons venir. Cette agrégation, liée par nos capacités cognitives, ne manque pas de concéder au présent une relative densité. Les « présents », loin de représenter des événements ponctuels juxtaposés les uns après les autres, se chevauchent et se fondent ensemble pour nous livrer toute la texture et la saveur que nous leur connaissons.
Ce texte de Jean-Sébastien Gonsette est publié sous la license CC BY-NC-ND 4.0
[25]: Ce calcul se base sur l’entropie S d’un trou noir de surface A et donné par la formule S=(k.A) / (4.lp2). Dans celle-ci, k est la constante de Bolzmann et lp est la longueur de Planck. Cette entropie est liée au nombre d’états possibles N par la formule S=k.log(N).
[26]: Celle-ci aurait pour effet d’offrir des directions privilégiées le long de ses axes, alors que l’espace est connu pour être isotrope.
[27]: C’est d’ailleurs ce à quoi s’emploie la théorie de la gravitation quantique à boucles. Celle-ci ne présuppose aucune structure d’espace-temps absolue préexistante, mais modélise l’univers par l’évolution d’un graphe quantique, ou mousse de spin, dans lequel chaque nœud représente un quanta d’espace.
[28]: D’après la théorie quantique des champs, une force est un concept qui naît de la capacité qu’ont les particules élémentaires à s’échanger de petits paquets d’énergie. Ce gain d’énergie pour l’une se réalise au détriment de l’autre et cela a pour effet de modifier la trajectoire de chacune d’elles. Mais cet échange ne se produit pas instantanément, il s’opère au travers de particules médiatrices de force que l’on appelle les bosons. Par exemple, le boson de l’électromagnétisme se révèle être le photon. Un boson est modélisé comme une perturbation se propageant au travers de ce que l’on appelle un champ quantique.
[29]: Nous parlons ici de causalité non classique, hors de l’espace et du temps, mais qui peut engendrer des événements se trouvant, eux, dans la lecture que nous en avons.