Wizium - My Crosswords Generator
The Long Way of Backtracking
Although the origin of Sudoku goes back as far as the last century, a surge of popularity can be noted during the year 2005. I remember it particularly well, because it was at that time that I discovered them while I was going to winter sports. I guess I had to come across a collection of grids at a gas station, during one of our stops to our destination. This totally new concept for me occupied me some time, the time to solve some grids. But the algorithmist in me quickly wondered what could be the iterative and deterministic procedure that should be applied to resolve a grid every time. It turns out that it is not very complicated if we allow ourselves to make assumptions and come back on them later. This method is at the basis of backtracking and this is our subject for today.
I have to admit that my interest in Sudoku dropped drastically once I finished my demystification work by mentally developing my little algorithm. I have never even coded it, so I cannot say for sure that I have not missed some subtleties. Because at that point, the game looked too simple and I focused on another idea. Of course, it must have been influenced by the crossword games that my magazine should also contain, but I distinctly remember thinking that generating such crossword grids automatically had to be a challenge on a whole new level. The basic principle of trial and error is certainly the same, but the space of possibilities is at a completely different scale and appeared to me to require a great deal of ingenuity.
A very hard start
As often with me, I can’t resist the challenges I throw to myself and, after taking advantage of the ski lifts to think about some preliminary ideas, I soon started to test them for real once back at home. But the difficulty of the problem far exceeded my expectations. I don’t hide from you that my first experiments were really bad. Imagine my first iterations with tiny grids of 9 squares out of 9 which filled laboriously until half, then interminably iterated over all possible combinations of these 4 or 5 words, without ever being able to place a 6th. The fourth word was at best updated every half hour and at that rate I could not envision the grid complete before a million years. So I’m not even talking about bigger grids, like the fairly well spread 17x17 format. Yes, the algorithm was correct from a formal point of view, in the sense that it would eventually discover a solution by going through all the possibilities, but from a practical perspective it was disastrous.
It soon became clear that several problems had to be overcome before hitting the road successfully, and that each of these points was decisive for reaching the holy grail of the high-performance generator.
- How to encode the dictionary of words and how to be effective to find candidates to place on the grid?
- What is the right order to place and test words on the grid?
- How to avoid as much as possible testing unnecessary combinations or, in other words, how to prune the tree of possibilities at best?
I will address these three questions one after the other, but first, let’s talk about backtracking itself to understand the context in which they fit.
The longest journey begins with a first step… maybe in the wrong direction
As mentioned on Wikipedia, backtracking refers to a family of algorithms for solving constraint satisfaction problems. This is a good thing, because that’s what it’s all about here: an empty grid must be filled with letters under the constraint that their sequences, taken horizontally or vertically, always correspond to a word in a pre-established list. A naïve implementation simply consists in enumerating all the possibilities until you find one that doesn’t violate any imposed rule.
To fix the ideas, I propose to ignore the black boxes at first and to concentrate on the generation of perfect squared grids, i.e. containing only letters. This problem offers the advantage of being able to both illustrate the principle of backtracking, but also to make you realize the abysmal complexity of the process as long as you try it with a brutal and naïve approach.
Let’s start with a very simple problem to easily enumerate all the solutions: consider a 3x3 grid to fill on the basis of a dictionary containing this rich list of French words: “QUE”, “UNS”, “EST” et “TES”.
Backtracking idea simply consists in inserting the elements one after the other, each time making a choice among all those respecting the desired constraints. Of course, there may sometimes be no possibility, which involves changing an item placed previously in order to enumerate new combinations. If this last element also comes to be exhausted, then we will go up a step further in the stack of items already in place, and so on. This method merely enumerates all the possible cases until it reaches a solution by chance. In the case of our little example, the combinatorial tree and the way to iterate through it are given below.
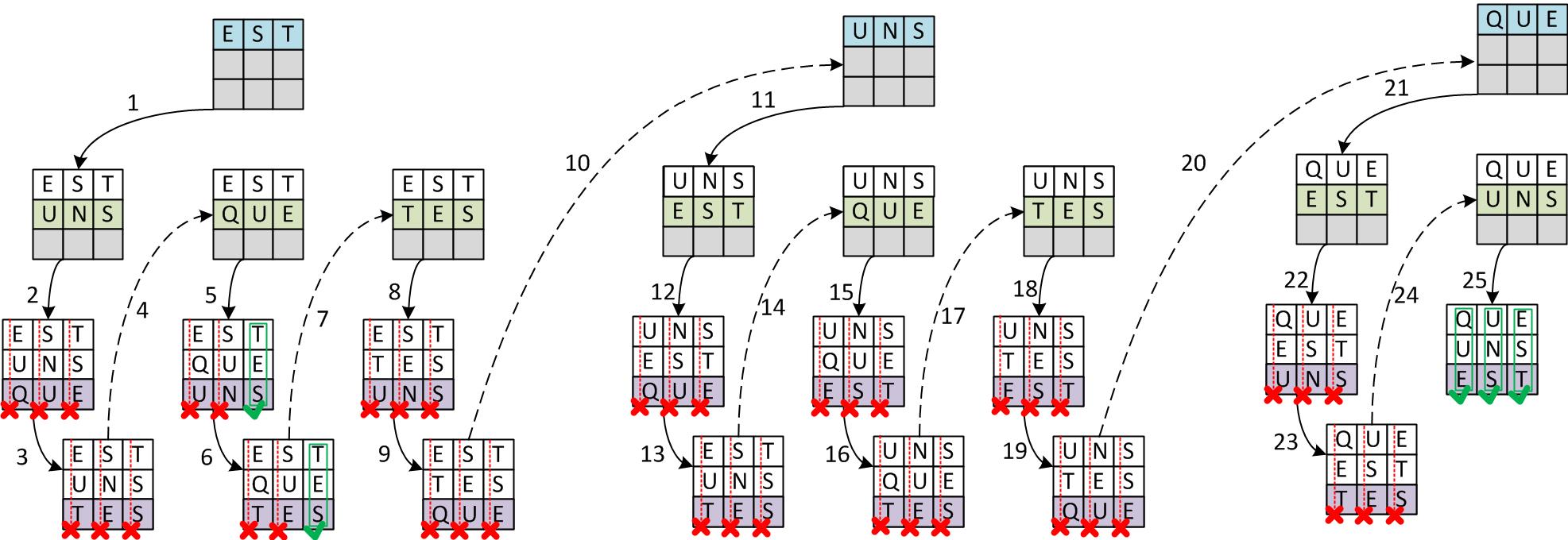
Illustration of the backtracking procedure. In this example, it just tests all the possible combinations.
For this exercise, we try to iteratively place three words horizontally, from top to bottom. As soon as the third word is in place, we check if the three vertical words then formed are in the dictionary. If this is not the case, the algorithm removes it from the grid and chooses a new option.
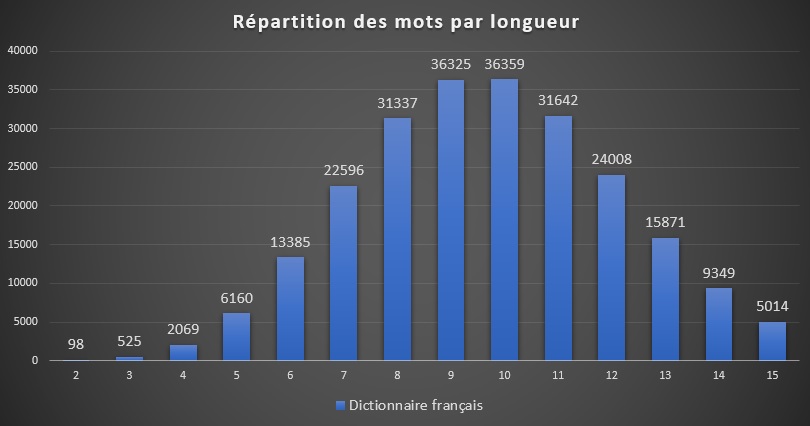
The procedure is systematic and guarantees to find the solution. Let us, however, try to evaluate the difficulty of such a problem according to a grid size $S$ and a dictionary containing $N$ words of size $S$. To clarify, here is the distribution of the words in my French dictionary spread according to their length.
It is necessary to stack $N$ words on each other before being able to check whether each of the $N$ vertical locations contains a valid word, if any. It is possible to estimate this probability easily if we ignore the correlations between sequences of letters. So if we take two words $w_1$ and $w_2$ randomly in the dictionary, the probability of coincidence between the $i^{th}$ letter of the first and the $j^{th}$ letter of the second is given by:
$$p_{co}=P(w_1[i]=w_2[j])=\sum_{l=1}^{26}f(l)^2,$$
where $f(l)$ corresponds to the frequency of occurrence of the $l^{th}$ letter of the alphabet. This frequency is simply determined by inspection of the words of the dictionary, as with the histogram below.
This gives a coincidence probability $p_{co}$ of 7.8%. A word of size $N$ in a column will then be valid if and only if this probability is favourable to us $S$ times in a row for any of the $N$ valid words in the dictionary. The probability $p_v$ of finding a correct word in any of the vertical locations is then:
$$p_v=1- (1 - p_{co}^S)^N $$
And for the probability that the complete grid is correct, it is given by:
$$p_g={p_v}^S = N^S.{p_{co}}^{S^2}$$
We can immediately see that this formula does not look very favourable for large grids. On the other hand, and it makes sense, the more the words in the dictionary, the greater our chances of finding a correct arrangement. But to get a clear idea of what this formula represents, let’s put a few figures on it right away:
| $S$ | $N$ | $p_g$ | Number of grids | Mean solving time |
|---|---|---|---|---|
| 5 | 6160 | $10^{-8.7}$ | $10^{19.0}$ | 2 minutes |
| 6 | 13385 | $10^{-15.0}$ | $10^{24.8}$ | 35 years |
| 7 | 22596 | $10^{-23.7}$ | $10^{30.5}$ | 10 billion years |
| 8 | 31337 | $10^{-34.8}$ | $10^{36.0}$ | 1000 trillion years |
| 9 | 36325 | $10^{-48.5}$ | $10^{41.0}$ | ??? |
| 10 | 36359 | $10^{-65.0}$ | $10^{45.6}$ | :'-( |
The first two columns give the size of the grid and the number of words of that length. The third column gives the probability that a grid assembled at random by stacking $S$ words is valid, while the fourth gives the total number of grids that can be generated in this way. Finally, the last column estimates the average time needed to find a correct grid at the rate of one million grids tested per second.
A first interesting observation comes from the comparison of the number of grids that can be generated with the probability that one of them is a solution. With the dictionary used to create this table, we are almost certain that no perfect grid of size 9 can be generated, the number of combinations being 10 million times too small to hope to find one. As for the size 8 grids, they should contain about fifteen solutions.
The second important point concerns the pantagruelic number of grids to be tested before one can hope to find a winning combination. For a grid of size 8, this value is around $10^{35}$ grids, which is similar to finding the right grain of sand among a volume of fine sand equivalent to that of the earth. This breathtaking analogy clearly shows that the method proposed here requires some adjustments, in order to generate perfect grids in less than one thousand trillion years.