Wizium - My Crosswords Generator
The Right Way to Pave the Grid
The method used previously to fill the grid was excessively naive, because it is quite catastrophic to wait the grid is full before to test the validity of the solution. The problem being combinatorial, the exponential nature of the combinations of words appears as so many branches and twigs subdividing frightfully quickly. So it is better to realize as soon as possible that the chosen path is rather a dead end, so as to cut off the dead branch as soon as possible and avoiding to lose valuable computing time in the depths of its tree.
But you still have to know what is the most effective way to proceed, so as to anticipate as quickly as possible any blocking situation. I do not pretend to have the ultimate answer to this question. However, I will simply present two possible methods, one of which is the one implemented in Wizum.
First method: the braiding
This technique is quite natural and consists of alternating the placement of words horizontally and vertically, from top to bottom and from left to right. The interleaving of words is then maximal and makes it possible to detect any deadlock very early. In that case, it is necessary to go back and change the previous word to remove the blocking point.
In the example above, using the French word CREOLE for the third vertical slot forbids the placement of any fourth horizontal word. There is indeed no solution of six letters starting with REO. This invalidates the previous word and immediately forces us to replace it with something that does not contain an O on the fourth row. All the remaining empty squares on the grid are then as so many combinations of words that don’t have to be tested.
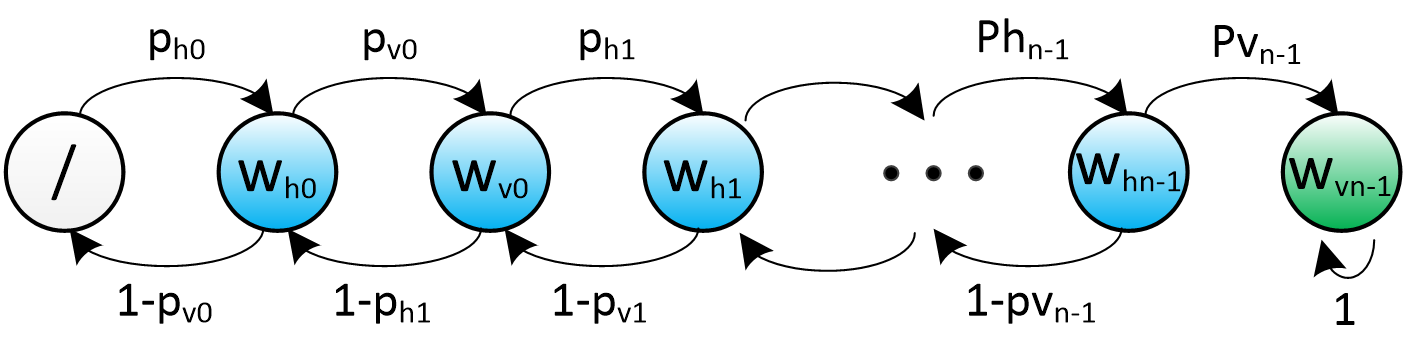
Let’s try now to evaluate the gain that this methodology can offer. It can be studied by approaching it like a discrete Markov chain, that is to say that the paving algorithm can be assimilated to a stochastic process whose state only depends on the current grid slot to fill in. The success or failure of this operation leads either to advance to the next word or, on the contrary, to go back to change the previous one. This process is not really homogeneous, because technically, the probabilities of transitions depend not only on the part of the grid that we are trying to fill, but also on all the combinations of letters that have already been exhausted. However, it’s sufficient to use this approximation as we only want to estimate the order of magnitude of the gain provided by this approach.
For that purpose, let call ${w_h}_i$ the $S$ horizontal slots and, in the same way, let call ${w_v}_i$ the $S$ vertical slots. The probability that some word in the dictionary fits each of these slots is given by:
$${p_{h}}_i = 1 - (1 - {p_{co}}^i)^N$$
$${p_{v}}_i = 1 - (1 - {p_{co}}^{i+1})^N$$
with $i=0…S-1$. These formulas simply reflect the probability that a certain number of randomly matched letters correspond to a valid word part. The higher is $i$, the lower the chances because of the increasing number of letters to deal with. We can then model the backtracking process by this Markov chain:
Without going too much into mathematical details, a Markov process can be studied through the properties of its transition matrix $P$. This one is constructed so that each element $(P)_{ij}$ is equal to the transition probability from state $i$ to state $j$.
$$P=\begin{pmatrix} 0 & 1-{p_v}_0 & 0 & 0 & 0\newline {p_h}_0 & 0 & \ddots & 0 & 0\newline 0 & {p_v}_0 & 0 & 1-{p_v} _ {S-1} & 0\newline 0 & 0 & \ddots & 0 & 0 \newline 0 & 0 & 0 & {p_v} _ {S-1} & 1 \end{pmatrix}$$
so that if $\phi(n)$ represents the probability distribution of the process state at time n, then the distribution at the next step will be given by:
$$\phi(n+1) = P. \phi(n)$$
The last state is called an absorbing state because it corresponds to the construction of a valid complete grid and stops the building process. This can be seen on the graph because of the unique transition probability of value 1 that cycles on this final state. This property is also found in the last column of the matrix $P$ which does not permit to redistribute the probabilities other than in the last state. Conversely, all other states are transient, as there is no guarantee that the algorithm will cross them more than once. Then, the value that is particularly interesting to study concerns the average time spent in these transient states before reaching the final state.
To achieve this, we first need to rewrite the matrix $P$ by highlighting this distinction, thanks to the square matrix $Q$ capturing this transient aspect, as well as to the vector $R$ representing the absorbing state.
$$P=\begin{pmatrix} Q & \boldsymbol{0}\newline R & 1\newline \end{pmatrix}$$
This representation enables to calculate the matrix $N = (I-Q)^{-1}$ by which it is possible find the average duration of the transient phase, or in other words, the average number of steps of the backtracking algorithm (follow this link for more information on this subject).
Now let’s look at the new estimates of the number of steps required to solve our perfect grids of different sizes, in order to appreciate the gain brought by this new method.
| $S$ | Number of grids | #naïve | #braiding | Mean slv. time |
|---|---|---|---|---|
| 5 | $10^{19}$ | $10^{8.7}$ | $10^{3.4}$ | 1ms |
| 6 | $10^{24.8}$ | $10^{15.0}$ | $10^{6.3}$ | 2s |
| 7 | $10^{30.5}$ | $10^{23.7}$ | $10^{11}$ | 1 day |
| 8 | $10^{36.0}$ | $10^{34.8}$ | $10^{17.8}$ | 20.000 years |
As before, the last column estimates the resolution time at a rate of one million tests per second. It goes without saying that the progress is spectacular, the resolution of a 7x7 grid can now be considered without problem, passing from 10 billion years (which is not far from the age of the universe) to just a single day. The 8x8 grids, however, remain out of reach with this method, at least with the usage of a conventional computer.
Second method: the scaffolding
The technique I am about to describe is the basis of the algorithm implemented in Wizium. It results primarily from a long search punctuated by many trials and many errors, not from the analysis you are reading, because it came much later. Despite its empirical elaboration, its main advantage is that it does not suffer from the same weaknesses than the previous method. It is much more direct and anticipates problems better. To realize this, let’s start by taking a look at the construction of the following grid:

Pathological construction by vertical vertical interleaving of words. It is only at the last stage of the algorithm that the impossibility of the last column is detected.
This pathological construction was custom-made, but nevertheless illustrates an inevitable flaw in the method of braiding: when we put the last words, the success of the operation is all about luck and nothing about anticipation. This is what can be seen in this example, the laying of the second horizontal word generates a deal-lock, because it prevents to place a word vertically on the last column. But there is nothing in the algorithm to detect this dead-end and it will continue laboriously to build a grid that is doomed to failure. It is only when looking for the last word that the procedure will start to go back to solve the situation, and it will have to undo almost the entire grid.
To avoid such kind of problems, it is necessary and sufficient to check that it is still possible to place a word vertically on each column each time a horizontal word is chosen. But in doing so, it is not needed anymore to place any word vertically. The stacking of horizontal words is sufficient as it is carried out in an enlightened way: the algorithm ensures continuously that we will not have a bad surprise at the end. So it is not question here of throwing words loose to hope to get out a valid grid at the end, it is rather about stacking words carefully at each step. It is of course possible that, anytime, no word in the dictionary satisfies the current constraint. But in this case, the blockage is identified at the earliest and allows to go back immediately, without embarking on a sterile search. This method is illustrated in the following animation.
In addition to its anticipation ability, this method requires placing only $S$ words on the grid, against $2.S$ words for the braiding method. This implies that the corresponding Markov graph is shortened and, if the transition probabilities are favorable, may be easier to get through.
Let’s study these transition probabilities. The approach is as follows: a horizontal word can be placed if there is at least one compatible vertical word on each of the crossed columns.First, we need to look a little more closely at this number of compatible words. It is certain that, the more we move on in the construction, the more this number decreases because of the higher length of the corresponding prefixes. For example, when I put the (French) word BRELER, I have to check that there is a word starting with HAB in the first column. This number of possibilities is higher than when we put the (French) word ETETER and that we have to check that there is a word starting with HABLE.
The average number of words available, given the length of a prefix, can be found by simply compiling some statistics about the dictionary used. This is the purpose of this script and the following graph illustrates some figures.
Let us define the function $M (S, i)$ expressing the average number of words available given a prefix length $i$. It allows us to calculate the probability that each letter of horizontal words placed at level $i$ still allows us to put a word vertically across.
$${p_ {co}}_i = 1 - (1-p _{co})^{M(S, i)}$$
The probability that a given word is compatible on each column is then given by ${{p_ {co}}_i}^S$, which finally makes it possible to calculate the probability of being able to place a word at level $i$:
$${p_ {h}}_i = 1 - (1-{{p _{co}} _i}^S )^N$$
Before going further, it is interesting to compare the two methods in terms of their probabilities of transition with concrete values. They are given in the following table for a grid of 6x6 squares. Not only does the scaffolding technique require fewer steps, but the probabilities are also higher.
| Stage | Braiding | Scaffolding |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 1 | 1 |
| 4 | 1 | 1 |
| 5 | 1 | 0.47 |
| 6 | 0.998 | 0.043 |
| 7 | 0.998 | |
| 8 | 0.39 | |
| 9 | 0.39 | |
| 10 | 0.038 | |
| 11 | 0.038 | |
| 12 | 0.003 |
Equipped with these new probabilities, we can again calculate the expectation of the transient phase to obtain an order of magnitude of the number of steps required to solve the grid by this second approach. However, it is important to mention that, here, it is necessary to correct the values we obtain. Indeed, the transition probabilities relate to the possibility that there is a word compatible with each of the crossed columns, but you have yet to find this word! This is by no means immediate since it may require several trials to achieve it. It is still possible to get there intelligently by keeping the count of all the incompatible letters, which makes it possible to exhaust the whole dictionary in a maximum of $26.S$ steps.
The table that follows compares the number of steps specific to the two methods exposed above with, for the last, a correction factor estimated at $10.S$.
| $S$ | # grids | #braiding | #scaff. | Mean slv time |
|---|---|---|---|---|
| 5 | $10^{19}$ | $10^{3.4}$ | $10^{2.8}$ | 0,5 ms |
| 6 | $10^{24.8}$ | $10^{6.3}$ | $10^{3.8}$ | 6 ms |
| 7 | $10^{30.5}$ | $10^{11}$ | $10^{5.7}$ | 0,5 sec. |
| 8 | $10^{36.0}$ | $10^{17.8}$ | $10^{8.5}$ | 5 min. |
Although this study is theoretical, the average number of steps to solve these perfect grids in Wizium is very close to the values displayed here. This shows how important the choice of the algorithm is when the search space of the problem to be treated is large. For the 8x8 grids, it allowed us to go from a resolution in one thousand trillion years to 20,000 years, then to a handful of minutes. It is a dizzying acceleration of no less than 26 orders of magnitude, which is more or less equivalent to reducing the size of a galaxy to that of a city and then to that of a bacteria.