iPendulum
Pendule inversé, part 1
Le concept de pendule inversé n’est ni nouveau ni inutile. J’en veux pour preuve que vous, lecteur, en êtes le parfait exemple. Un corps humain est un pendule inversé ! En effet, en regardant la définition sur Wikipedia nous pouvons lire : un pendule inversé est un pendule dont le centre de masse est placé au-dessus de son point de pivot. En d’autres termes il s’agit d’un pendule que l’on a mis la tête en bas et qui ne demande qu’à se casser la figure.
Le centre de gravité de votre corps étant situé au niveau de votre nombril, il se situe bel et bien au-dessus du point de pivot constitué par vos chevilles. Cela implique que dès que votre nombril se déplace un peu trop vers l’avant ou l’arrière, vous devriez choir. Pourtant me direz-vous, vous ne vous cassez pas (trop souvent) la figure. C’est vrai, mais aussi naturel que cela vous semble, cela n’est possible que grâce à de nombreux organes internes collaborant afin de vous maintenir sur vos jambes. Typiquement, vos yeux et votre système vestibulaire travaillent de concert pour indiquer à votre cerveau comment vous êtes orienté dans l’espace. Celui-ci peut alors calculer les ajustements nécessaires pour rectifier tout déséquilibre, sous forme d’impulsions nerveuses envoyées vers les muscles adéquats.
En fait, quoique cela soit plus facile à faire qu’à dire, tous les pendules inversés reposent exactement sur ce principe. Pourtant, voir un pendule inversé (non biologique) à l’œuvre suscite toujours l’étonnement, voire l’émerveillement. Cela trouble assurément notre sens de la logique et de ce qui semble naturel. En effet, les objets inanimés sont généralement incapables de telles prouesses et nous n’y sommes ainsi jamais confrontés. Aussi, j’espère susciter votre étonnement avec ce pendule qui est non seulement capable de tenir en équilibre sur un tout petit point de pivot, mais qui est aussi capable de se relever tout seul.
Un pendule ! Oui, mais lequel ?
Pour être honnête, je ne savais même pas au départ que ce que je désirais construire s’appelait un pendule inversé. J’avais bien l’image du Segway en tête, mais je ne connaissais pas la dénomination générique exacte. Heureusement, il n’a pas fallu longtemps à Google pour me révéler le terme correct après avoir commencé mes recherches avec des termes du genre « truc qui tient en équilibre à l’envers ». Cela a ensuite été très vite. Il vous suffit de taper « pendule inversé » dans YouTube pour vous faire submerger par dix ans de vidéo sur le sujet. Il est vrai qu’il s’agit d’un sujet universitaire récurrent, car il permet aux étudiants de tester toutes sortes de techniques de régulation, de se frotter à un sujet multidisciplinaire, et de provoquer à tous les coups un wôw effect.
Il y a donc des modèles pour tous les goûts : cela va du modèle deux roues à la Segway (j’en ai même vu en Lego), à la barre (voir double ou triple barre) en rotation autour d’un chariot se mouvant sur un rail, en passant par le quadricoptère supportant une tige sur laquelle est placée un verre. Le problème récurrent de toutes ces réalisations est qu’aucune ne peut fonctionner décemment sur mon bureau, entre ma souris et mes factures. Au mieux il faut trop d’espace pour le faire fonctionner, au pire, il n’est pas autonome et il faut sortir une alimentation et autres artilleries de laboratoire pour le mettre en branle. Enf ait, mes critères de conception étaient :
- Petite dimension (une dizaine de cm) et léger ;
- Complètement autonome, c’est-à-dire que le pendule doit embarquer sa propre batterie ;
- Simple, afin de démythifier le principe général sans ajouter de complexité superflue.
C’est alors que je suis tombé sur un projet plutôt épatant réalisé par l’équipe de scientifiques de l’Institut ETH Zurich pour les Systèmes et le Contrôle Dynamiques, le Cubli. Le Cubli est un cube étonnant capable de tenir en équilibre sur l’une de ses arrêtes ou sur l’un de ses coins, en sautant pour passer d’une position à une autre. Je vous invite à visionner leur vidéo qui décrira, bien mieux que les mots, les exploits de ce petit cube robot.
Si le Cubli respecte bien mes deux premiers critères, j’ai eu quelques doutes concernant le 3e point. Le fait qu’il dispose de trois degrés de liberté afin de se déplacer et maintenir son équilibre dans toutes les directions rend la modélisation un peu ardue. De plus, les équations de mouvement sont joliment non linéaires, ce qui n’arrange pas les choses pour les lois de contrôle qui doivent le piloter. Toutefois, si la généralisation en 3D est complexe, le principe de base en 1D est simple à comprendre et à modéliser.
D’un cube, je suis donc passé à un carré (avec un peu d’épaisseur bien sûr) capable de maintenir son équilibre autour d’un seul axe. Ensuite, comme je n’étais pas spécialement intéressé par le fait que mon carré puisse « rouler », je l’ai encore coupé en deux et le modèle a pris sa forme triangulaire définitive. Même si toutes ces coupes limitent beaucoup les capacités de mouvement du pendule, elles offrent tout de même l’avantage d’une simplification et d’un gain de poids considérable. Comme nous le verrons plus tard, ce gain de poids permet au pendule d’être beaucoup plus agile et de pouvoir maintenir son équilibre de façon plus robuste.
Anatomie d’un pendule inversé
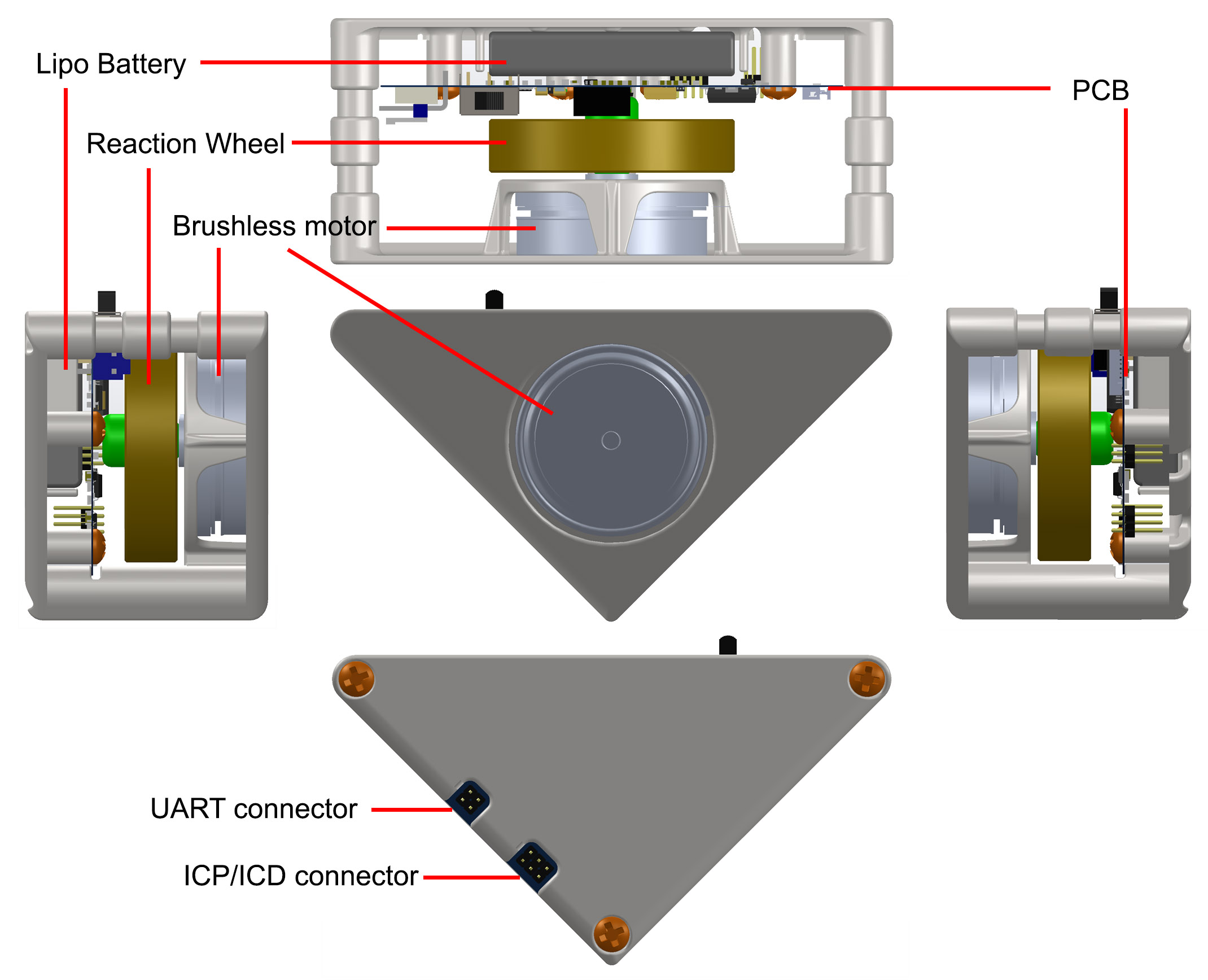
Après ce long préambule, vous pouvez légitimement vous dire que je ne vous ai finalement pas encore appris grand-chose et que vous ne savez toujours pas quels sont les principes physiques à l’œuvre dans ce pendule. Je vais y venir, mais pour ça il faut que nous allions d’abord jeter un coup d’œil dans les entrailles de la bête. La figure quis uit vous donne une vue éclatée des différents éléments. Nous pouvons y voir que le pendule est assemblé à partir d’un nombre assez restreint de constituants.
Le squelette du pendule est assuré par deux demi-coques en plastique, conçues pour pouvoir être imprimées en 3D. Nous reviendrons sur ce point dans le dernier article de cette série. La première demi-coque sert de support au circuit imprimé, tandis que la deuxième assure le maintien du moteur et de sa roue d’inertie. Le circuit imprimé renferme toute l’intelligence du pendule au sein d’un microcontrôleur PIC, mais doit également assurer la commande moteur et la conversion de puissance nécessaire pour l’alimenter à partir d’une batterie. La batterie en question est du type LIPO, tel que largement prisé en modélisme. Elle se glisse directement dans un support prévu pour elle derrière le PCB. Le moteur est l’unique organe de commande du pendule. Il se loge dans une niche prévue à cet effet dans la coque en plastique. Sur ce moteur vient se greffer une roue d’inertie en couplage direct, dont le rôle sera expliqué très bientôt. Cette roue d’inertie est constituée d’un axe en plastique, également imprimé en 3D, sur lequel vient se sertir un anneau métallique dont la masse apporte l’inertie désirée.
Comment ça marche ?
Tout comme pour le Cubli, le pendule que je vous propose repose sur le principe physique de la conservation du moment angulaire d’une roue d’inertie pour assurer son équilibre. La différence fondamentale vient du nombre de ces roues : trois dans le Cubli, pour une seule dans le cas qui nous occupe. Il faut également préciser que, même si la roue d’inertie en rotation vous fait penser à une toupie et à son effet gyroscopique, ce dernier n’est absolument pas en cause ici.
L’explication de la conservation du moment angulaire nécessite peut-être de vous ramener un peu en arrière, sur les bancs d’école du cours de physique. C’est là que l’on vous a sûrement expliqué les lois du mouvement de Newton, ces grands principes de base concernant le mouvement des corps :
-
Dans un référentiel galiléen (c.-à-d. soumis à aucune force extérieure), le vecteur vitesse du centre d’inertie d’un système est constant si et seulement si la somme des vecteurs force qui s’exercent sur le système est nulle. Ce principe exprime que la quantité de mouvement d’un corps se conserve si aucune force n’est appliquée dessus.
-
Dans un référentiel galiléen, la somme des forces s’exerçant sur un système est égale à la dérivée de la quantité de mouvement. Il s’agit de la célèbre formule $\sum_i \vec f_i = {\vec dp \over dt}$, ou plus vulgairement, $f=m.a$. Ce principe exprime que la quantité de mouvement d’un corps ($p=mv$) est modifiée au prorata de la résultante des forces qu’il subit.
-
Tout corps A exerçant une force sur un corps B subit une force d’intensité égale dans la même direction, mais de sens opposé. Ce principe est aussi connu comme le principe d’action-réaction. Il traduit également le fait que la quantité de mouvement ne peut pas disparaître. Ce qu’un corps gagne, l’autre le perd ; un peu comme quand vous effectuez un transfert d’argent d’un compte vers un autre, ce n’est jamais perdu pour tout le monde.
Ces principes sont tout à fait généraux et il est nécessaire de les transformer un peu dès qu’ils sont appliqués à un système constitué de plus qu’une particule. En effet, il est très commode de ne pas avoir à manipuler la position de chacune d’elles, car leur nombre devient très vite gigantesque. À la place, une seule position est manipulée, appelée centre de gravité du système, auquel est également ajoutée l’orientation angulaire du système autour de ce point. Cette décomposition purement pratique a pour effet de scinder les forces en deux catégories : les composantes qui modifient la quantité de mouvement linéaire du centre de gravité du système, et les composantes qui modifient la quantité de mouvement angulaire du système autour de son centre de gravité.
Lorsque cette décomposition est réalisée mathématiquement, il apparaît que les forces qui modifient la quantité de mouvement angulaire se manipulent plus facilement en faisant intervenir la notion de couple. Un couple n’est jamais que la composante d’une force mettant en rotation un système autour d’un point, multipliée par la distance qui sépare ce point de rotation au point d’application de la force. Une fois cette notion introduite, il est possible de faire apparaître une analogie directe entre les lois concernant la modification de la quantité de mouvement linéaire par des forces, et les lois concernant la modification de la quantité de mouvement angulaire par des couples. Cette analogie est résumée dans le tableau suivant :
Armés de ces principes et de ces définitions, nous sommes maintenant pleinement en mesure de décrire ce qu’il se passe au niveau du pendule. Le fonctionnement est en fait pratiquement identique aux volants d’inertie embarqués dans les engins spatiaux. Imaginez un satellite en orbite autour de la terre qui doit corriger son orientation afin de réaligner correctement ses antennes vers un point précis de la terre. Nous pouvons supposer qu’avant de réaliser sa manœuvre, son moment angulaire est nul (il ne tourne pas sur lui-même). S’il applique alors un couple moteur sur l’un de ses volants d’inertie, ce volant va accélérer sa rotation dans un sens ; mais dans le même temps le reste du satellite va subir un couple de grandeur égale et de sens opposé (3e principe). Il va dès lors se mettre à tourner dans le sens contraire. Même sans aucun point d’appui extérieur dans l’espace, un satellite peut ainsi s’appuyer sur son volant d’inertie interne pour modifier son moment angulaire. Si nous regardons le satellite complet (volant d’inertie inclus), l’absence de couples externes implique aussi que le moment angulaire total ne peut pas changer, c’est-à-dire qu’il doit rester nul (2e principe). Cela est bien le cas, car la somme du moment angulaire du volant d’inertie (disons positif) plus le moment angulaire du reste du satellite (négatif) ne change jamais si les seuls couples en jeu sont des couples entre des constituants internes. Pour revenir à l’analogie sur les comptes en banque, sans apport d’argent externe, vous aurez beau transférer de l’argent entre votre compte courant et vos comptes épargnes dans tous les sens, vous ne deviendrez jamais plus riche.
La situation est pratiquement identique pour le pendule, mais avec la contrainte que le couple extérieur n’est pas nul à cause de l’action de la gravité. Aussi, si vous essayez de maintenir tel quel le pendule sur sa pointe, la gravité aura pour effet de transformer le moindre déséquilibre en une accélération angulaire non nulle, jusqu’à ce qu’il s’écrase au sol. Le seul moyen de contrer la gravité est d’amener le centre de gravité du pendule exactement au-dessus de son point de pivot. Comme ce point est petit, cette opération n’est pas possible en pratique. Par contre, il est tout à fait possible d’amener le centre de gravité du pendule au-dessus du pivot, en moyenne. Ainsi, c’est en tirant le pendule vers la gauche quand il dévie vers la droite, et inversement, qu’il est possible de le maintenir en équilibre et de contrer l’action de la gravité. C’est là que le moteur et sa roue d’inertie entrent en jeu. Comme pour le satellite, il est possible de faire accélérer le corps du pendule dans un sens en accélérant sa roue d’inertie dans l’autre sens. Cela revient, à chaque instant, à mesurer par où tombe le pendule et à en déduire la valeur du couple moteur à appliquer pour compenser le déséquilibre. Si la commande est bien réalisée, le pendule décrira de petites oscillations, tantôt vers la gauche, tantôt vers la droite, mais ne tombera pas.
Et pour le saut alors ?
La capacité du pendule à sauter, pour passer depuis sa position couchée à sa position d’équilibre, est assurément surprenante. Pourtant, l’explication est plutôt simple. Une fois dévoilée, elle vous laissera la même impression que la révélation d’un tour de magie qui semblait tellement extraordinaire. Le principe consiste tout bonnement à accélérer la roue d’inertie dans la direction vers laquelle nous voulons sauter, jusqu’à ce qu’elle atteigne la vitesse adéquate. À ce moment, il suffit de bloquer la roue pour que tout le pendule décolle. Nous pouvons une fois encore appeler Newton à la rescousse pour expliquer les détails du phénomène. Quand il est au sol, roue à l’arrêt, le moment angulaire du pendule est nul. Il est toutefois capable d’accélérer sa roue d’inertie et gagner ainsi en moment angulaire en s’appuyant sur ce sol. C’est grâce à cet appui que l’opération est possible, cela ne fonctionnerait pas dans l’espace. Une fois une vitesse de rotation suffisante acquise, bloquer la roue revient à faire passer son moment angulaire à zéro. Toutefois, nous avons vu que le moment angulaire d’un système isolé se conserve et ne peut pas disparaître, il faut donc le transférer quelque part. Et ce quelque part, c’est le pendule lui-même ! Concrètement, bloquer la roue revient à exercer un grand couple sur celle-ci pour la faire décélérer rapidement. Ce couple a pour effet d’extraire le moment angulaire de la roue. Or, le troisième principe nous dit qu’un couple opposé va être exercé sur l’organe de freinage (lié au pendule), transférant ainsi le moment angulaire vers celui-ci. L’opération est blanche si nous prenons un point de vue externe et considérons le pendule et sa roue comme un tout. Au départ, le moment angulaire provenait de la rotation de la roue, tandis qu’il provient de la rotation du pendule lui-même après le freinage. Mais le moment angulaire total, lui, ne change pas.
Électronique du pendule
Je pense que nous avons fait assez de théorie pour cette fois-ci. Je donnerai plus de détails sur les lois de contrôle lors du prochain article. En attendant, il est temps de vous mettre quelque chose de concret sous la dent. C’est pourquoi je vous propose d’examiner l’électronique embarquée du pendule. D’un certain point de vue, il s’agit peut-être de la partie la plus simple, car nous restons ici dans du très classique.
L’électronique du pendule doit assurer quatre grandes fonctions :
- Convertir la puissance issue de la batterie LIPO afin d’alimenter le moteur brushless ;
- Délivrer les signaux de commande adéquats pour faire tourner le moteur brushless ;
- Mesurer la dynamique du pendule au moyen d’un accéléromètre et d’un gyroscope ;
- Implémenter la loi de commande du moteur dans un microcontrôleur en fonction des valeurs retournées par les capteurs.
La tension délivrée par la batterie LIPO varie entre 7 V et un peu plus de 8 V en fonction de son état de charge. Le moteur Maxon, quant à lui, fonctionne avec une tension nominale de 12 V. Une alimentation à découpage articulée autour d’un circuit MAX668 (U300) a dès lors pour but de réaliser l’adaptation de puissance nécessaire. Étant donné que le moteur absorbe un courant de 2 A pour un couple de 55mNm, l’alimentation doit être capable de fournir au moins le double d’intensité. L’alimentation suit un schéma de régulateur Boost classique. Lorsque la broche 8 de U300 est à l’état haut, le transistor de puissance T300 conduit et cela a pour effet de faire grimper l’intensité du courant passant à travers de l’inductance de puissance L300. La diode D300, elle, empêche que le condensateur de sortie C307 ne se décharge par la même occasion. Lorsque la broche 8 passe à l’état bas, le condensateur se bloque, obligeant ainsi l’énergie magnétique accumulée dans L300 à se déverser dans C307 au travers de la diode. U300 régule les cycles de ce processus à une fréquence configurable, qui est ici fixée à 300 kHz au travers de R300. Cette régulation se base sur la tension de sortie prélevée aux bornes de R203 et R302, ainsi que sur le courant circulant dans l’inductance et mesuré à travers de R301. La tension de sortie v12 contient immanquablement des ondulations hautes fréquences dues aux charges et décharges répétées de C307. Cette ondulation est toutefois dominée par la valeur de sa résistance série équivalente (ESR) et des courants hautes fréquences qui la traversent. C’est pourquoi un soin tout particulier doit être apporté à la sélection de ce condensateur.
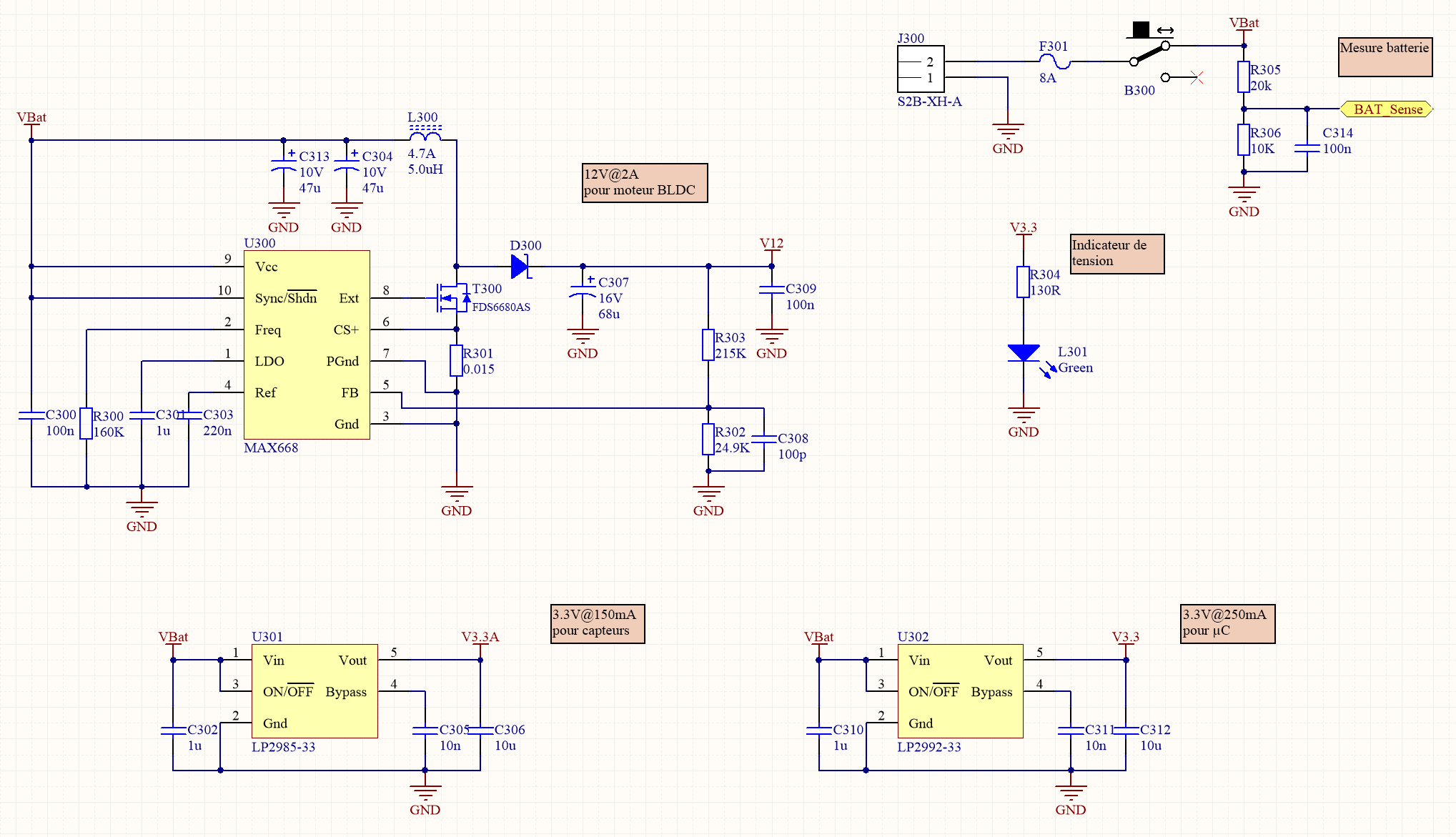
Schématique de l'alimentation à découpage du pendule, ainsi que des alimentations linéaires secondaires.
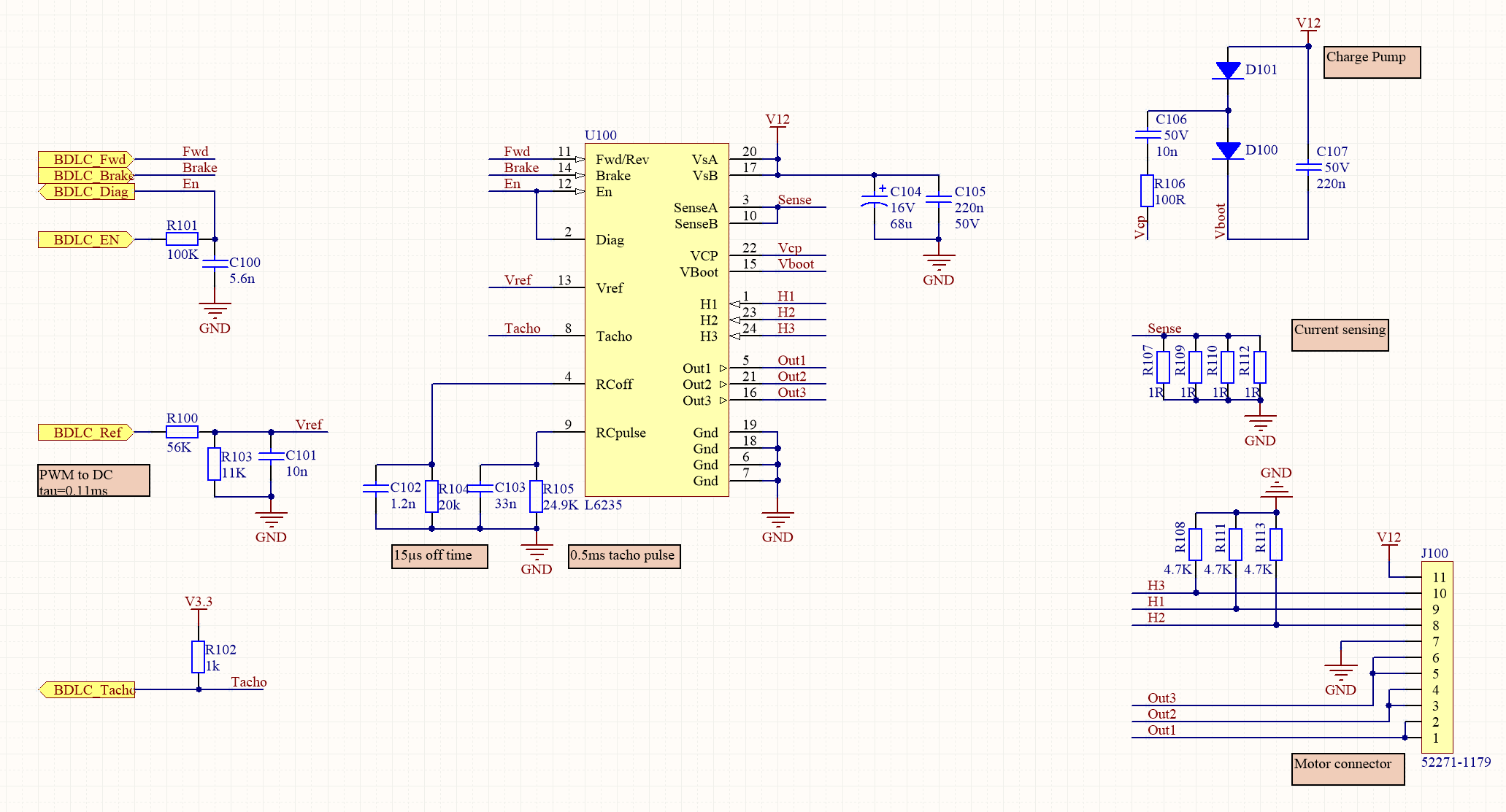
Le moteur sélectionné pour ce projet est un moteur sans balais (brushless) de la série EC Flat de chez Maxon. Par rapport à un moteur DC traditionnel, l’absence de balais évite une usure mécanique prématurée et des bruits électromagnétiques associés. Il permet en outre une meilleure conversion de puissance. D’un autre côté, il souffre d’un prix de construction plus élevé ainsi que d’une logique de commande bien plus complexe. En effet, il est nécessaire d’alimenter un tel moteur via trois phases, en permutant les flux magnétiques de celles-ci au rythme de rotation précis du rotor. Dit simplement, on ne peut pas juste faire tourner le moteur brushless en le connectant à une source de tension. Il est nécessaire de disposer d’un système électronique pour superviser la séquence d’alimentation des bobines. C’est ici que le circuit intégré L6235 (U100) entre en jeu. Ce dernier contient toute la logique pour piloter un tel moteur, y compris les transistors de puissance. Il se pilote par un ensemble d’E/S relativement simples. « Fwd/Rev » permet de choisir le sens de rotation souhaité, « Brake » active la fonction de freinage électromagnétique (c’est cette fonction qui permet au pendule de sauter), « En » permet d’activer la rotation du moteur, « Vref » est une entrée analogique permettant de choisir la limite de courant délivré au moteur, « Diag » signale le déclenchement d’une protection interne et enfin, « Tacho » délivre les impulsions tachymétriques. La sélection de limite de couple se réalise par la conversion d’un signal PWM en tension analogique grâce au filtre passe-bas constitué par R100, R103 et C101. La connexion aux trois phases du moteur est effectuée sur les trois sorties « Out1 » à « Out3 », tandis que les signaux de position issus des capteurs à effet hall du moteur sont décodés sur les entrées « H1 » à « H3 ». Le circuit contrôle le courant absorbé par le moteur en le mesurant au travers des résistances R107, 109,110,112 et en le comparant à la consigne fixée sur « Vref ». Ce circuit permet bien de contrôler le couple délivré puisque le couple d’un tel moteur est proportionnel au courant absorbé.
Le pendule ne peut acquérir le sens de l’équilibre qu’en étant capable de mesurer sa position dans l’espace et de corriger cette position en conséquence. Il doit donc être doté de capteurs permettant de lui indiquer quel est l’angle qu’il forme avec le sol. Ces capteurs sont constitués d’un gyroscope 1 axe, matérialisé par le circuit ISZ-2510, et d’un accéléromètre 3 axes embarqué dans le circuit ADXL345. Nous verrons dans le prochain article comment il est possible de reconstruire les paramètres dynamiques du pendule en fonction de ces mesures. Ces deux circuits sont en fait des capteurs analogiques intégrés dans un circuit numérique. Ils disposent ainsi de deux entrées d’alimentation distinctes. La raison d’être de ces deux entrées est liée à la mesure analogique qui doit être le moins possible polluée par les bruits numériques du reste du circuit. Les deux circuits dialoguent avec le microcontrôleur via un bus SPI.
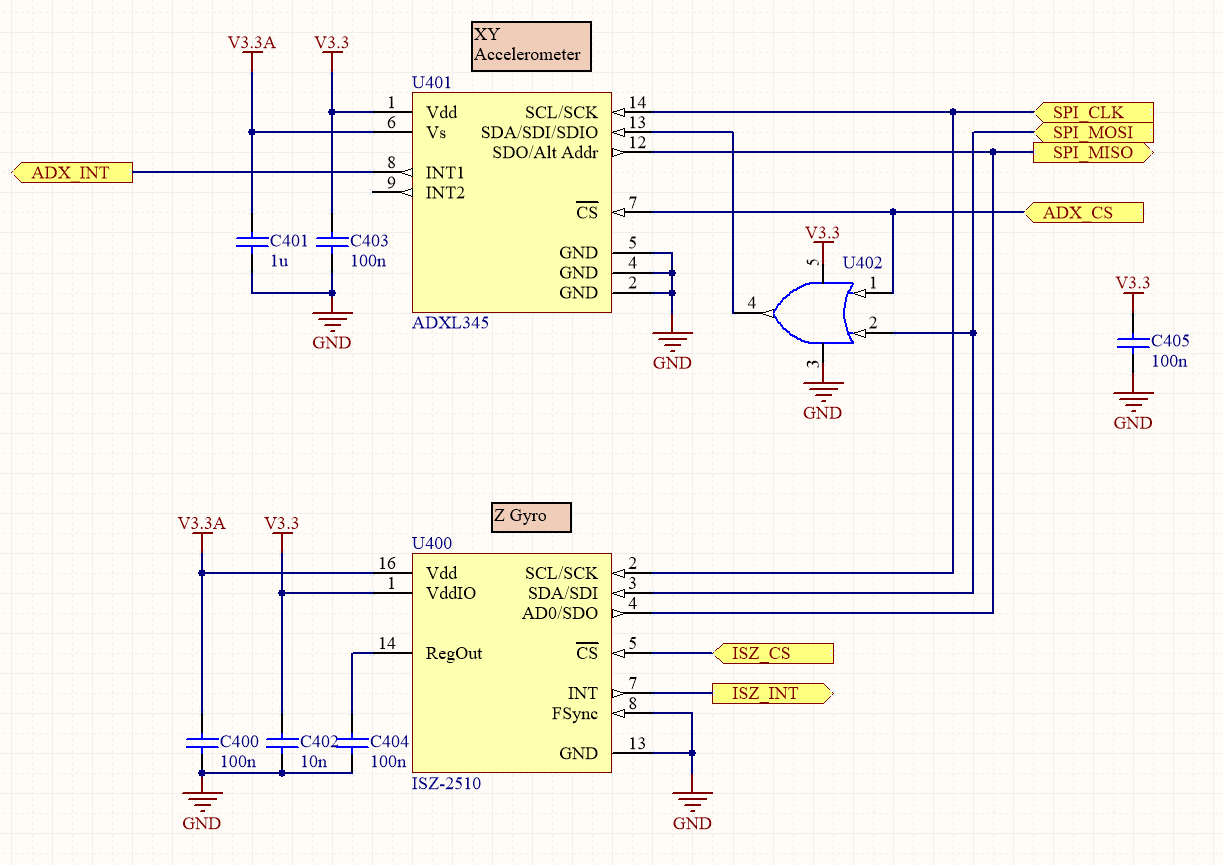
Schématique des capteurs mesurant le mouvement angulaire du pendule, ainsi que des vecteurs d'accélération.
Toute l’intelligence du pendule est embarquée dans un microcontrôleur dsPIC de 16 bits. Par rapport aux PIC32, la famille 16 bits est idéale dans un projet tel que celui-ci où la réactivité prime sur la puissance de calcul. De plus, l’espace mémoire offert en RAM et ROM est assez généreux et permet le développement d’applications plus complexes que sur une famille 8 bits. Enfin, les dsPIC bénéficient également de sorties PWM qui sont utilisées dans ce projet pour commander le moteur. Le microcontrôleur se programme de manière classique via son interface ICD/ICP reliée au connecteur P200. L’une de ses UART est utilisée pour réaliser un port série au travers du circuit SN65C3221 (U201).