Lors de l’article précédent consacré à ce pendule inversé, je vous ai expliqué les principes physiques généraux qui sont à l’œuvre pour maintenir l’équilibre du pendule et le faire sauter lorsqu’il est couché sur le flanc. Cependant, si vous désirez comprendre les détails techniques de fonctionnement ou si vous désirez vous plonger dans le code pour réguler le pendule à votre sauce, ces explications sont loin d’être suffisantes. Je vous propose donc aujourd’hui de retrousser vos manches et de vous plonger gaiement avec moi dans le cambouis de la régulation LQR, des filtres de Kalman et des systèmes temps réel.

Avant de pouvoir prétendre réguler l’état d’un système, il faut d’abord le comprendre et avoir une bonne idée de son fonctionnement. C’est ce que l’on appelle un modèle, c’est-à-dire un ensemble de concepts qui capturent les caractéristiques essentielles et font abstraction des détails. Dans le cas de la régulation d’un système physique comme le pendule, cela implique d’établir les lois de mouvement qui régissent sa dynamique en fonction des commandes qui lui sont appliquées. L’intérêt d’une telle modélisation est multiple. Premièrement, elle permet d’étudier plus finement le problème que l’on cherche à résoudre. Elle permet ensuite de dimensionner correctement les différents éléments en étudiant l’impact de chacun d’eux. Par exemple,

• quelle taille raisonnable le pendule doit-il avoir ?
• Quel poids de batterie pouvons-nous embarquer ?
• Quel couple le moteur doit-il délivrer ?
• Quelle puissance le PCB doit-il délivrer au moteur ?
• Etc.

Ces questions sont nombreuses et se mordent la queue assez rapidement puisque chaque élément a finalement une conséquence sur un autre. Quand on part de rien comme dans le cas présent, le mieux est d’y aller au pifomètre en fixant arbitrairement certains paramètres, puis en vérifiant qu’au final le tout tient la route. Un modèle peut être ensuite implémenté en simulation. Cela permet de gagner énormément de temps en testant les hypothèses de dimensionnement sur PC et en visualisant directement le résultat des lois de régulation sur de jolis graphiques (voir le graphe ci-dessous issu d’une simulation). Dans mon cas, je n’ai lancé la phase de prototypage qu’une fois sûr que tout tenait la route en simulation. Bien sûr, ce n’est pas 100% bulletproof, car certains détails vous échapperont toujours, mais ça limite tout de même fortement les risques d’aller dans le mur. Le dernier point, et non des moindres, est que ce modèle est indispensable pour les algorithmes embarqués dans le pendule. Il permet tout d’abord de paramétrer les lois de contrôle qui commande le moteur du pendule, ensuite, il est nécessaire pour interpréter correctement les données retournées par les capteurs et réaliser une estimation correcte de l’état du pendule à un instant donné.

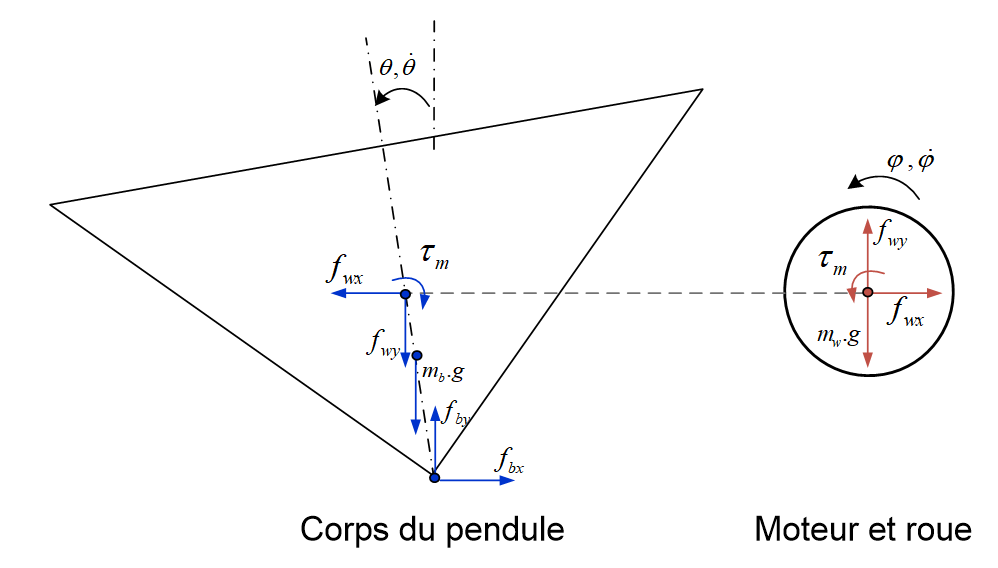
Les équations de la dynamique du pendule s’établissent en déterminant le nombre de degrés de liberté du système, en dressant la liste exhaustive des forces et couples qui agissent sur chacune des parties, en écrivant les effets dynamiques de chacun d’eux, puis en secouant le tout pour ne garder que les paramètres qui nous intéressent. Ici, le pendule a deux degrés de liberté : le corps du pendule qui pivote autour de son point de contact avec le sol, d’angle $\theta$, ainsi que la rotation du moteur et sa roue d’inertie, d’angle $\varphi$. Le but du jeu est de retrouver comment évoluent les dérivées secondes de ces deux paramètres, c’est-à-dire leur accélération, en fonction du couple délivré par le moteur. La figure qui suit reprend la liste de tous les paramètres agissant sur le corps du pendule et sur sa roue.

Pour la roue il y a bien sûr le couple moteur lui-même $\tau_m$, le couple de frottement entre le rotor et le stator $\tau_f$, et aussi les deux forces qui maintiennent le rotor en place $f_{wx}$ et $f_{wy}$. Pour le pendule, il y a d’abord les forces et les couples agissant sur la roue, mais dans le sens opposé. Il y a ensuite les deux forces entre le pendule et le sol $f_{bx}$ et $f_{by}$, qui maintiennent le pivot du pendule en place. Finalement, la gravité $g$ agit à la fois sur la masse du pendule $m_b$ sur la masse de la roue $m_w$. Les calculs qui s’ensuivent ne sont pas essentiels à la compréhension des phénomènes. Tous calculs faits, nous pouvons trouver les deux équations dynamiques suivantes :

$$\ddot\theta = {M.g.sin \theta - \tau_m + \tau_f \over I}$$ $$\ddot\varphi = {(I+I_w).(\tau_m - \tau_f) \over I.I_w} - {M.g.sin \theta \over I}$$

Dans lesquels $m_b$, $I_b$, $m_w$ et $I_w$ expriment les masses et inerties du corps du pendule et de sa roue d’inertie, tandis que $l_b$ et $l_w$ traduisent la hauteur du centre de gravité du corps du pendule et la hauteur de la roue d’inertie par rapport au sol. Ces équations peuvent être facilement intégrées pour simuler le pendule, mais vont surtout nous servir ici pour établir les lois de contrôle du moteur.

Stabilité du pendule

Pas besoin d’être bac+7 pour se rendre compte que, tel quel, le pendule n’est pas stable. Si vous le lâchez depuis sa position d’équilibre…, il tombe. Cependant, il est vraiment intéressant de comprendre ce que signifie être instable d’un point de vue mathématique, afin de pouvoir décrire la stratégie qui va nous permettre de stabiliser le pendule. Pour cette explication, je vais me rabattre sur un exemple qui a le mérite d’être très simple tout en capturant l’essence du problème de la stabilité. Faisons donc un peu de biologie avec une boîte de Petri. Une telle boîte permet la mise en culture de micro-organismes afin d’étudier leur évolution. Imaginons que le nombre d’organismes dans la boîte soit donné par la variable $y$. Imaginons également que les taux de naissance $n$ et de décès $d$ de ces organismes soient simplement proportionnels à la taille de cette population. Nous pouvons donc écrire :

$$y'=n.y-d.y$$

Si les taux sont constants, l’intégration de cette équation est aisée et le résultat nous donne l’allure de l’évolution de la population. Pour une population de départ $y_0$ nous obtenons :

$$y(t)=y_0.e^{(n-d).t}=y_0.e^{\lambda .t}$$

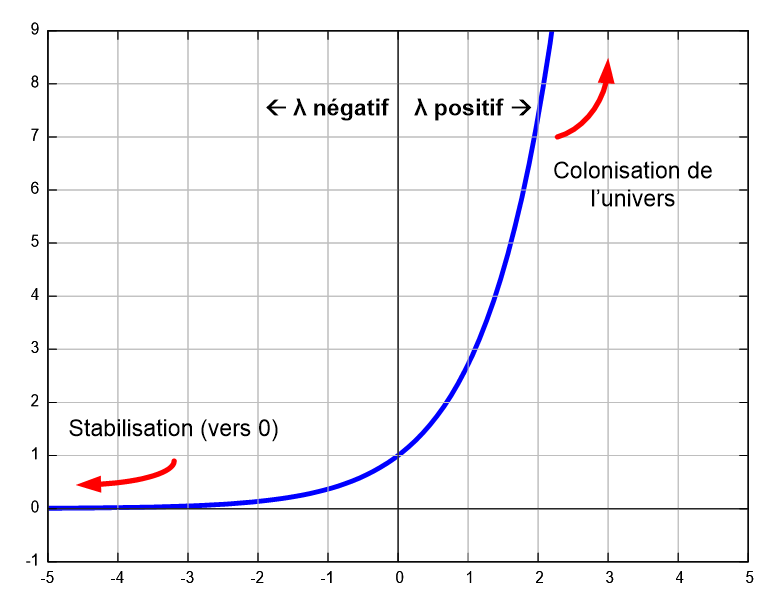
La nature de la fonction exponentielle nous montre bien que, selon le signe de $n-d$, l’évolution de la population va prendre une allure radicalement différente. Si le taux de décès est supérieur au taux de naissance, l’exposant est négatif et la population va s’éteindre progressivement. Dans l’autre cas, la population va croître sans fin et coloniser l’univers (du moins si les équations ont encore du sens à cette échelle). L’exposant $\lambda$ à l’œuvre dans cette équation est aussi appelé la valeur propre du système. C’est le signe de cette valeur propre qui détermine si le système est stable (valeur propre négative) ou instable (valeur propre positive). Un système instable tend toujours à « exploser » du fait qu’il s’écarte sans fin de toute valeur de repos (figure ci-dessous).

Imaginons maintenant que nous puissions contrôler arbitrairement le taux de croissance/décroissance, en manipulant le pH de la solution par exemple. De plus, faisons en sorte que ce contrôle soit proportionnel à la quantité d’individus dans la boîte. Nos équations d’évolution deviennent alors :

$$y'=n.y-d.y+k.y$$ $$y(t)=y_0.e^{(n-d+k).t}$$

Et là réside toute l’astuce de la manœuvre. Comme le paramètre $k$ peut être choisi librement (dans les limites physiques du système bien entendu), il est possible de forcer une valeur propre positive à devenir négative, ce qui permet à un système de retrouver sa stabilité.

Cette digression étant faite, revenons-en au pendule. Les équations qui régissent son comportement sont un peu plus compliquées que dans l’exemple précédent. Les différents états du système, comme l’angle et la vitesse du pendule ou la vitesse du moteur, doivent être empaquetés dans des vecteurs, tandis que les multiples équations différentielles doivent être poussées dans des matrices. Au final, on se retrouve à calculer les valeurs propres d’une matrice et il est alors bien moins évident de voir pourquoi le système est stable ou pas. Toutefois, l’idée de base reste exactement la même. Si l’une des valeurs propres est positive, alors quelque chose de la forme $e^{λ.t}$ apparaîtra quelque part dès que vous intégrerez votre système, et plus rien n’ira comme vous voulez.

Qui dit régulation dit PID…

… mais pas cette fois. Le régulateur PID est certainement le plus utilisé dans l’industrie. Il permet de contrôler une grandeur physique en boucle fermée, en comparant cette mesure avec une consigne, puis en calculant une commande par intégration, par dérivation et par proportionnalité de l’erreur mesurée. Son avantage réside dans sa simplicité et son universalité. Différentes méthodes empiriques existent pour régler les trois coefficients du régulateur afin d’obtenir la rapidité, la précision et la robustesse nécessaire. En fait, le principal défaut vient du fait qu’un PID fonctionne très bien s’il se limite à un système à une entrée de commande et une variable de sortie (Single Input Single Output - SISO). Or, nous avons vu que dans notre cas nous avions deux degrés de liberté, l’angle du pendule et la vitesse de rotation de la roue d’inertie. Ces deux grandeurs doivent être contrôlées en ensemble par une seule entrée de commande, le couple moteur. Un PID n’est donc pas approprié ici. Bien sûr, vous pourriez argumenter que la seule chose qui compte c’est de contrôler l’angle du pendule, et que la vitesse de rotation de la roue n’a pas d’importance. Un seul PID pourrait donc bien faire l’affaire. Oui…, sauf que la vitesse de rotation du moteur n’est pas si anodine que ça. Un moteur ne peut délivrer un couple que dans une plage de vitesse de rotation donnée. Dès lors, si nous ne régulons pas cette vitesse de rotation, elle va lentement dériver jusqu’à atteindre des valeurs non acceptables et le pendule ne sera plus contrôlable.

Régulation par retour d’états

Le type de régulation à l’œuvre dans le pendule s’appelle de la régulation par retour d’états. Contrairement au contrôleur PID qui travaille dans le domaine fréquentiel, ce type de régulation boucle sur la valeur des états internes du système. Concrètement, le bouclage s’effectue en introduisant un coefficient de gain réel pour chaque possibilité de retour d’une sortie sur une entrée. Dans le cas du pendule, les états que nous contrôlons sont l’angle du pendule, la vitesse de rotation du pendule et la vitesse de rotation de la roue d’inertie. Il comprend donc trois sorties. La boucle de rétroaction s’effectue dès lors au travers de trois gains qui sont ensuite additionnés et appliqués sur l’unique entrée de commande (figure ci-dessous).

La régulation par retour d’états fonctionne, car il est possible de montrer que, moyennant certaines conditions de contrôlabilité, il est possible de calculer des valeurs de gains telles que les valeurs propres du système contrôlé deviennent toutes négatives. Comme nous l’avons vu, des valeurs propres négatives sont les garantes de la stabilité d’un système. Nous pouvons aussi noter au passage que, dans le cas où le système ne contient qu’un seul état, nous retombons sur notre exemple de boîte de Petri.

Il reste juste un petit détail à régler, comment calculer ces fameux gains pour stabiliser le pendule ? Différentes approches sont possibles, mais une méthode assez commode consiste à utiliser la théorie appelée Linear Quadratic Regulator (LQR). Celle-ci aboutit à un algorithme permettant de calculer automatiquement la valeur de ces gains, en fonction des équations du système et d’une série de coefficients de poids. Ces poids doivent être définis par le concepteur lui-même et représentent l’importance que l’on accorde aux différents états du système et à la commande lors de la régulation.

Plus un poids est important, plus l’algorithme optimisera l’état ou la commande associé. Celui-ci convergera alors plus rapidement vers sa valeur de consigne. Dans le cas du pendule, nous ne sommes pas particulièrement intéressés par l’obtention de performances extraordinaires en ce qui concerne la stabilisation. Par exemple, cela ne change pas grand-chose s’il compense un déséquilibre en trois secondes plutôt qu’une seule. Par contre, ce qui nous intéresse est d’arriver à rétablir un déséquilibre avec un minimum de couple. En effet, le couple du moteur est limité et il est intéressant de pouvoir en tirer le maximum, en étant capable de compenser le plus grand déséquilibre possible. C’est pour cela que les gains du pendule ont été calculés en mettant un poids infini sur la commande, et zéro sur les poids correspondant aux états. Cela revient à calculer le régulateur à énergie de commande minimum.

J’ai bien conscience de n’avoir que gratté la surface de l’iceberg qu’est la théorie du contrôle. La littérature sur ce sujet est large, mais plutôt technique. En ce qui me concerne, j’ai trouvé très instructive la série de tutoriels proposée par l’université du Michigan et consacrée au contrôle de systèmes avec Matlab. L’un des tutoriels propose d’ailleurs la régulation d’un pendule inversé.

Estimation de l’état du pendule

Obtenir les gains nécessaires pour stabiliser notre pendule grâce à un régulateur par retour d’état est une chose, mais encore faut-il connaître à chaque instant quels sont les états du pendule : angle du pendule, vitesse du pendule et vitesse du moteur. Deux principes différents sont possibles pour estimer l’état d’un processus. Le premier consiste à le prédire, alors que le deuxième consiste à le mesurer.

Prédire l’état du pendule est possible si l’on connaît son état de départ, ainsi que la façon dont il bouge selon la consigne de couple que l’on applique sur son moteur. En intégrant les équations différentielles de son modèle, nous pouvons ainsi déduire où il va se trouver un instant plus tard et répéter ce processus à chaque pas de temps. Pour établir une analogie: c’est un peu comme essayer de conduire une voiture les yeux fermés, en se basant sur votre modèle mental de la route et du comportement de la voiture. Ça peut effectivement fonctionner pendant quelques secondes, avant que vous ne vous crachiez sur un arbre et deviez admettre que votre modèle mental ne devait pas être aussi parfait qu’escompté. Ce que je veux illustrer par cet exemple n’est pas que réaliser une prédiction soit mauvais en soi, mais que les différentes erreurs de modélisation auront pour conséquence que votre estimation va rapidement diverger de la réalité. Ce principe n’est ainsi valide que pour une période de temps limitée.

D’autre part, la façon la plus évidente d’obtenir l’état du pendule consiste sans aucun doute à le mesurer. Mais il ne faut pas croire pour autant que cette méthode est parfaite. Un capteur de mesure, quel qu’il soit, a une certaine imprécision et est de plus sujet aux bruits de mesure. En d’autres termes, deux mesures successives d’un état identique ne donneront pas deux fois le même résultat. De plus, il n’est pas toujours possible de tout mesurer. Selon le processus, certains états devront être déduits indirectement.

D’un côté nous avons donc une méthode précise à court terme, mais dont l’erreur diverge rapidement, et de l’autre nous avons une méthode dont la plage d’erreur est fixe, mais non négligeable. L’idéal serait de pouvoir être éclectique et d’utiliser l’une ou l’autre méthode en fonction de qui offre l’erreur la plus faible. Prenons un exemple qui illustre ces propos : imaginez que vous et votre collègue deviez mesurer la valeur d’une résistance. Vous effectuez la mesure chacun séparément et obtenez respectivement 68 et 70 Ohms. Il semble raisonnable d’effectuer la moyenne de ces valeurs, car, statistiquement, les erreurs devraient se compenser. Imaginons maintenant que vous ayez une information supplémentaire. Le voltmètre que vous avez utilisé est du haut de gamme, alors que celui de votre collègue a couté 10 € au magasin de bricolage du coin. Dans ce cas vous seriez plus enclin à vous fier à votre propre mesure. Mais cela ne veut pas dire que la mesure de votre collègue est à jeter. Ce qu’il convient en fait de faire consiste à réaliser une moyenne pondérée des deux valeurs avec des poids calculés au prorata de la précision de chacun des instruments. Plus l’instrument est précis, plus le poids à utiliser pour moyenner est élevé. C’est exactement ce dont nous avons besoin pour combiner intelligemment les deux estimations de l’état de notre pendule. La prédiction faite suivant le modèle et la mesure obtenue des capteurs pourraient ainsi être pondérées en fonction de leur validité respective.

Filtre de Kalman

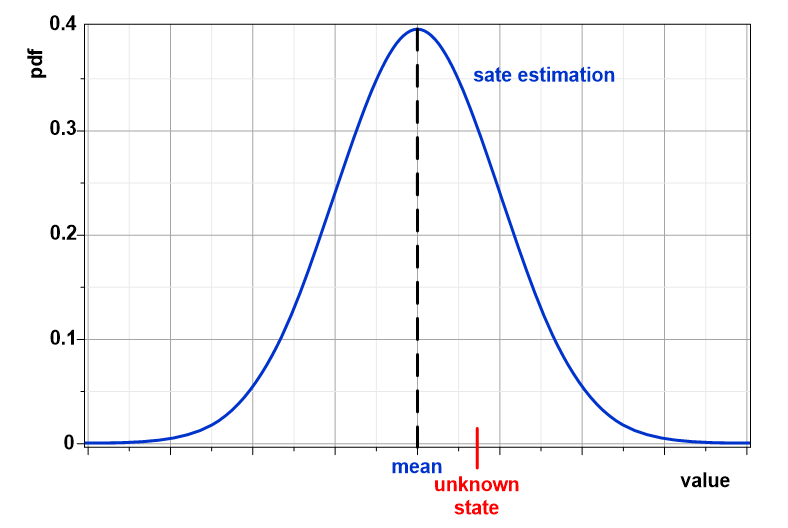
Le processus que je viens de décrire constitue le cœur du filtre de Kalman. Il s’agit d’un filtre sur les états qui effectue une moyenne pondérée des différentes mesures et prédictions d’un processus dynamique. Le but du filtre est d’ôter au maximum le bruit qui entache les mesures et les prédictions afin d’obtenir une estimation optimale de l’état de ce processus. Concrètement, le filtre de Kalman peut être décomposé en deux étapes. La première consiste à utiliser le modèle du système, ainsi que les commandes produites à un instant t, pour réaliser une prédiction de l’état du système au temps $t+dt$. La prédiction estime aussi comment l’incertitude courante sur l’état du système évolue en fonction de l’incertitude sur le modèle lui-même. Toutes les incertitudes d’un filtre de Kalman sont approximées par des gaussiennes. Pour un système qui ne contient qu’un seul état, la gaussienne est la courbe classique représentée à la figure ci-dessous.

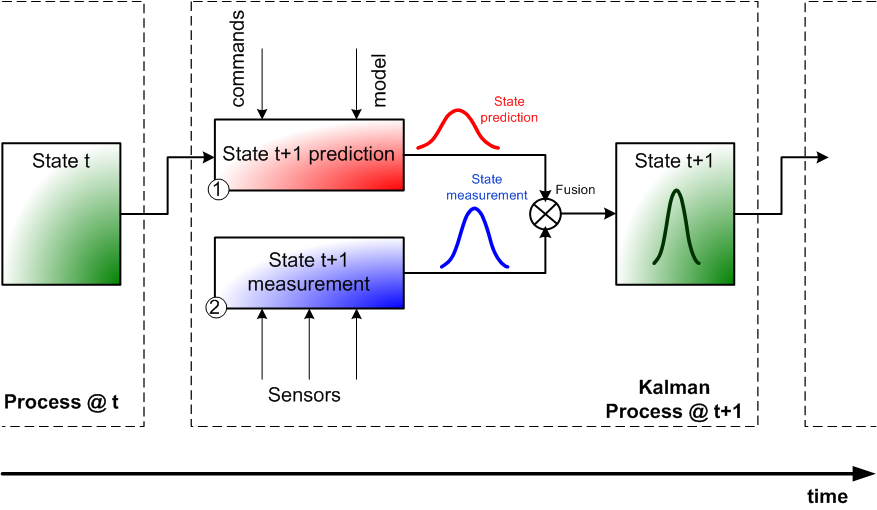
Dans les autres cas, cela devient une multigaussienne en plusieurs dimensions. La deuxième étape consiste à mesurer l’état du système au temps $t+dt$. Ces mesures viennent aussi avec leur lot d’incertitudes, une fois encore modélisées par des gaussiennes. Toutes les mesures sont pondérées par leur incertitude respective, comme dans l’exemple du voltmètre. Ensuite, le résultat est fusionné avec la prédiction en tenant compte là encore des incertitudes respectives des deux estimations. Une vue synthétique du processus est illustrée sur la figure qui suit. Si le sujet vous intéresse, je vous conseille vivement la lecture de ce livre.

Dans notre cas, les capteurs en œuvre pour l’estimation de l’angle que fait le pendule avec le sol sont un gyroscope et un accéléromètre. Le gyroscope ne comporte qu’un seul axe orienté dans la direction Z, perpendiculaire au circuit imprimé. L’accéléromètre comporte trois axes, X, Y et Z, mais seuls les deux premiers sont utilisés dans le filtre de Kalman. Ce dernier est plutôt rudimentaire, mais fournit un résultat amplement suffisant. Les deux capteurs sont fusionnés de la manière suivante. Le gyroscope fournit la vitesse de rotation du pendule. Par intégration sur un pas de temps $dt$, il permet de réaliser une prédiction de l’angle futur du pendule. L’accéléromètre, quant à lui, mesure principalement comment l’accélération due à la gravité est projetée sur les axes X, Y. Par inversion trigonométrique, il donne donc directement une mesure de l’angle que fait le pendule avec le sol. La prédiction et la mesure sont ensuite fusionnées comme vu précédemment, au prorata des erreurs de chacun des capteurs. L’estimation de la vitesse de la roue suit le même principe. Le couple que l’on impose au moteur permet de réaliser une prédiction sur l’accélération ou la décélération de la roue, et donc sur sa vitesse après un pas de temps $dt$. Cette prédiction est ensuite fusionnée avec la mesure de vitesse effectuée à chaque fois qu’une impulsion tachymétrique est réceptionnée.

Logiciel embarqué

Le logiciel embarqué dans le microcontrôleur PIC constitue la partie la plus musclée du projet. En effet, c’est ici que se cristallisent toutes les règles, modèles et équations qui permettent au pendule d’exister. De plus, il y a toutes sortes de mécanismes à gérer en arrière-plan pour que tout son petit monde interne puisse prendre vie : communication avec les capteurs, application des consignes de couple moteur, communication avec le PC via une UART pour remonter les télémétries, etc. La boucle de régulation en elle-même impose quelques contraintes. En effet, le pas de temps de numérisation est de l’ordre d’une dizaine de ms. Même si la charge de calcul n’est pas très élevée, le logiciel doit être très réactif. Aussi, tout le logiciel qui n’est pas dans cette boucle de régulation, comme la communication UART, doit pouvoir fonctionner en étant interrompu régulièrement.

L’écriture classique d’un tel programme sur un processeur nu n’est pas sans difficulté. L’approche élémentaire consistant à établir une super-boucle principale, appelant tour à tour tous les modules, n’est possible que quand le nombre de ces modules n’est pas trop élevé. De plus, cela devient vite un casse-tête quand les périodicités de chacun ont des ordres de grandeur différents. Typiquement, si vous avez une boucle de traitement rapide qui doit coexister avec une boucle de calcul plus lente en arrière-plan, vous devrez réfléchir à comment concilier les deux : temps partagé coopératif, utilisation d’interruptions, etc. Si en plus vous désirez exploiter les mécanismes d’économie d’énergie du processeur en le mettant en sommeil quand il n’y a rien à faire, cela devient vite un véritable enfer. Dans tous les cas, ce n’est viable qu’à petite échelle, car on se retrouve vite à devoir faire le travail d’un OS à la place d’un OS.

Un RTOS, quant à lui, offre l’avantage de pouvoir organiser son code de façon beaucoup plus modulaire. Chaque partie de l’application peut tourner indépendamment les unes des autres dans sa propre tâche et c’est à l’OS qu’il revient de faire les découpages temporels en arrière-plan pour donner l’illusion que toutes les tâches tournent en même temps. De plus, l’OS offre toutes sortes de moyens structurés pour faire communiquer les tâches entre elles (j’entends par là, en évitant l’emploi d’horribles variables globales). Par rapport à un OS traditionnel, les caractéristiques d’un RTOS sont légèreté et réactivité. Leur empreinte mémoire est très faible et ils peuvent ainsi être déployés sans difficulté sur de petits microcontrôleurs. Pour toutes ces raisons, le micrologiciel du pendule tourne sur un petit RTOS maison appelé NanoScale.

Architecture

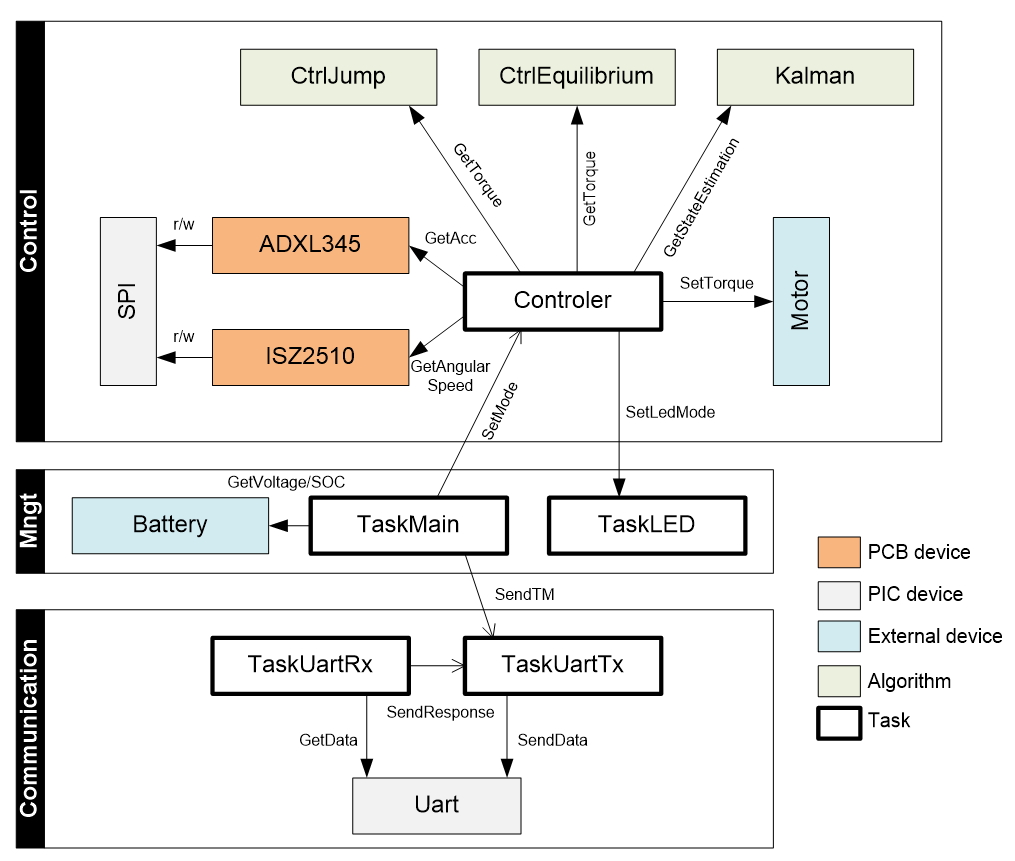
L’architecture générale de l’application embarquée sur le pendule est donnée à sur la figure qui suit. On peut y isoler les trois sous-systèmes suivants : communication, contrôle et management général. Le sous-système de communication a la charge de gérer la communication avec le monde extérieur au travers d’une interface série. Une tâche s’occupe de réceptionner les commandes, tandis qu’une deuxième collecte toutes les demandes de transmission de l’application et envoie les messages correspondants un à un. La tâche d’envoi réalise en fait un multiplexage temporel des messages à envoyer. Ceux-ci peuvent être, soit des réponses à des commandes entrantes, soit des télémétries envoyées spontanément. Le sous-système de contrôle est chapeauté par une tâche haute priorité activée toutes les 10 ms. À chaque activation, elle a la charge d’acquérir les valeurs des capteurs, d’estimer l’état du pendule correspondant, puis d’obtenir le couple moteur à appliquer en fonction de l’algorithme en cours de fonctionnement. Ces algorithmes représentent chacun une fonction élémentaire du pendule : saut, équilibre statique, balancement autour de la position d’équilibre, etc. Enfin, le sous-système de management implémente la logique générale du pendule. C’est lui qui active ou désactive le sous-système de contrôle, qui vérifie l’état de charge de la batterie, ou qui s’occupe d’activer ou faire clignoter les LED.

Initialisation et abstraction du microcontrôleur

Toute l’initialisation du contrôleur se fait dans le module Board Support Package (BSP.c). Cette opération consiste tout d’abord à configurer la fréquence de cadencement de l’horloge interne, ainsi que toutes les E/S nécessaires pour attaquer les différents périphériques du circuit imprimé. Elle initialise également quatre pilotes de périphériques : un bus SPI, une UART, un pilote pour l’accéléromètre ADXL345 et un pilote pour le gyroscope ISZ2510. Ces deux derniers pilotes utilisent le bus SPI pour communiquer avec leur homologue électronique sur le circuit imprimé. Enfin, c’est aussi ici qu’est réalisée l’initialisation du RTOS. Le module BSP a en plus la charge de proposer une couche d’abstraction permettant d’isoler le microcontrôleur du reste de l’application. Ainsi, c’est dans ce module que se trouvent toutes les routines de traitement d’interruptions. En particulier, l’interruption INT2 est reliée à la broche de sortie tachymétrique du contrôleur moteur. Celle-ci délivre une impulsion à chaque huitième de tour du moteur, ce qui permet d’en déduire sa vitesse. Enfin, l’abstraction repose sur un ensemble d’API spécifiques au PCB. Le module propose donc des fonctions bas niveau pour piloter les LED, simuler une EEPROM dans la mémoire flash interne, lire la tension de la batterie ou encore pour piloter le contrôleur moteur.

Interfaces externes

Le module battery.c est relativement simple. En plus de la lecture brute de la tension de la batterie via une entrée analogique du microcontrôleur, il offre également une correction de la valeur lue sur base d’un facteur de calibration. C’est aussi dans ce module que la charge restante de la batterie est estimée, en fonction de la tension et du courant débité.

Le module motor.c offre des interfaces permettant de donner des consignes au moteur via le circuit intégré L6235. Concrètement, ce dernier se charge de réguler l’intensité du courant circulant dans les bobines du moteur BLDC en fonction d’une valeur de consigne fixée par un signal analogique Vref. Comme le couple d’un tel moteur est proportionnel au courant qui le parcourt, ce circuit intégré fait théoriquement tout le travail pour nous lorsque nous avons à fixer une consigne de couple durant la régulation du pendule. Toutefois, un petit bémol est apparu en cours de développement, car il s’avère que ce circuit intégré ne fonctionne pas en mode quatre quadrants. Cela signifie concrètement qu’il ne peut réguler le couple que quand celui-ci est orienté dans le même sens que la rotation de la roue. De plus, il n’est pas capable de réaliser sa régulation pour de petites consignes de couple.

Le premier problème est pleinement résolu en utilisant une technique de commande originale du circuit L6235. Celle-ci consiste à envoyer un signal PWM sur sa broche Fwd. Normalement cette broche est utilisée pour choisir le sens de rotation du moteur. En y appliquant un signal PWM, le pont en H pilotant le moteur est basculé très rapidement et cela a pour effet de moduler la tension effectivement appliquée au moteur au prorata du rapport cyclique choisi. Consulter ce document pour plus d’informations sur la technique mise en œuvre. En cherchant un peu, je suis arrivé à trouver une combinaison de signaux qui permet finalement de réguler un couple négatif, c’est-à-dire un couple qui a pour effet de décélérer la roue.

Le deuxième problème est plus épineux et n’est pas encore résolu de manière satisfaisante. Pour le moment, je me contente de contourner la régulation du circuit L6235 lorsque de petites valeurs de couple sont nécessaires. J’utilise pour ce faire la technique de modulation de la tension expliquée précédemment, en me basant sur la courbe théorique de fonctionnement du moteur. Cela permet au final d’obtenir un couple moteur moyen pour un pas de temps de régulation $dt$. Le résultat n’est cependant pas à la hauteur du fait d’une discontinuité lorsque le sens de rotation du moteur s’inverse. Cela empêche pour le moment de réguler le pendule autour d’une vitesse de roue nulle.

Pilote des capteurs

Le pilote du capteur ADXL345 se trouve dans le module homonyme ADXL345.c. Celui-ci offre une API basique reflétant les fonctions offertes par le circuit intégré lui-même : sélection de la vitesse de transmission des données, mode d’économie d’énergie, etc. Le pilote s’appuie sur l’utilisation du pilote de bus SPI pour communiquer avec son capteur en émettant les trames ad hoc. La fonction principale est bien sûr celle qui permet de remonter les dernières valeurs d’accélération lues sur les 3 axes : ADXL345_GetAccelerations. Les accélérations sont exprimées en $mg$. Le pilote du capteur ISZ2510 fonctionne de façon tout à fait similaire et se trouve sans surprise dans le module ISZ2510.c. De la même manière, sa fonction principale est celle remontant la dernière valeur de vitesse angulaire : ISZ2510_GetAngularSpeed. Cette vitesse est exprimée en millièmes de $°/s$.

Tâches

Le travail du microcontrôleur est réparti en différentes tâches de criticités différentes. C’est à l’OS qu’il revient d’effectuer l’ordonnancement en basculant sans cesse l’exécution sur la tâche active ayant la priorité la plus haute. La tâche ayant la plus basse priorité est logiquement celle qui s’occupe de l’animation des trois LED : TaskLED.c. Chacune des LED est associée à un petit automate fini permettant de les faire clignoter séparément ou de façon synchronisée.

Par ordre de priorité vient ensuite la tâche de gestion TaskMain.c. Au démarrage, celle-ci commence par s’assurer que toutes les fonctions internes du pendule sont en ordre de marche : contrôle du moteur et réponse correcte des capteurs. Si tout est en ordre, elle active la tâche de contrôle et se met ensuite en attente de chaque fin de cycle de celle-ci. Dès que la fin d’un cycle est signalée, toutes les 10 ms, elle récolte toutes les données d’intérêt et les envoie dans des trames de télémétrie au travers de l’UART. Ces données sont constituées des valeurs renvoyées par les capteurs, de l’état estimé par le filtre de Kalman, et finalement des consignées envoyées au moteur pour la régulation. En plus de cela, la tâche vérifie aussi toutes les minutes que la tension de la batterie n’est pas descendue en dessous de ce qui est acceptable pour une batterie LIPO.

La tâche TaskUartTx.c a la charge d’envoyer toutes les données sortant du pendule vers l’UART. Ces données sont des messages qui peuvent être soit des réponses à des commandes, soit des télémétries. Un module désirant envoyer un message l’ajoute dans une FIFO, et ceux-ci sont ensuite dépilés un par un par cette tâche pour être envoyés sur l’UART.

La tâche TaskUartRx.c s’occupe de traiter toutes les commandes entrantes sur l’UART. Ces commandes permettent d’obtenir des informations relatives à l’état du système lorsqu’elles ne sont pas envoyées automatiquement dans les télémétries : état de l’OS, état de la batterie, etc.

La tâche la plus critique est finalement celle qui s’occupe de la régulation du pendule toutes les 10 ms : Controller.c. Un cycle de régulation est constitué des étapes suivantes : acquisition des valeurs des capteurs (accéléromètre et gyroscope), estimation de l’état du pendule en fonction de ces valeurs au travers d’un filtre de Kalman, calcul de la consigne de couple à appliquer au moteur en fonction du mouvement en cours d’exécution et, enfin, application de la consigne motrice. Le filtre de Kalman est implémenté dans le module, KalmanFree.c. En fonction du mouvement effectué, le calcul du couple moteur est réalisé dans le module CtrlEquilibrium.c ou CtrlJump.c.

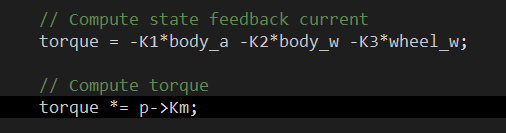
Pour l’anecdote, Sebastian Thrun (l’homme derrière la Google Car) explique dans l’un de ses cours quelles sont les quelques lignes de code qui constituent la substantifique moelle du système de localisation de la célèbre voiture. Plus modestement, vous trouverez ci-dessous les deux lignes de code qui calculent à chaque instant le couple qu’il faut délivrer au moteur pour maintenir l’équilibre du pendule. Le reste n’est que du détail, mais il ne faut pas perdre de vue que justement: le diable se cache dans les détails.