Wizium - Mon générateur de mots croisés
La longue voie du backtracking
Même si l’origine du Sudoku remonte aussi loin que le siècle dernier, un sursaut de popularité peut être noté durant l’année 2005. Je m’en souviens particulièrement bien, car c’est à cette époque que je les ai découverts, alors que je me rendais aux sports d’hiver. J’imagine que j’ai dû tomber sur un recueil de grilles dans une station-service, lors de l’un de nos arrêts en voiture vers notre destination. Ce concept nouveau pour moi m’a occupé quelque temps, le temps de résoudre quelques grilles. Mais l’algorithmicien qui sommeille en moi s’est vite demandé quelle pourrait être la procédure itérative et déterministe qu’il faudrait appliquer pour résoudre une grille à tous les coups. Il s’avère qu’elle n’est pas très compliquée pour peu que l’on s’autorise à émettre parfois des hypothèses et à revenir dessus par la suite. Cette méthode est à la base du backtracking, ou retour sur trace en bon français, et c’est d’elle que nous allons parler aujourd’hui.
Je ne vous cache pas que mon intérêt pour les Sudoku est drastiquement retombé une fois que j’eus fini de les démythifier en mettant au point mentalement mon petit algorithme. Je ne l’ai même jamais codé et je ne peux donc pas affirmer avec certitude que certaines subtilités ne m’aient pas échappées. Car arrivé à ce stade, le jeu m’apparaissait trop simple et c’est là qu’a germé une autre idée. Bien sûr, cela a dû être influencé par les jeux de mots croisés que mon magazine devait également contenir, mais je me souviens distinctement m’être dit que générer une telle grille de mots automatiquement devait être un défi d’un tout autre niveau. Le principe de base du backtracking consistant à procéder par essais et erreurs est certes le même, mais l’espace des possibilités est d’un tout autre ordre de grandeur et m’apparaissait nécessiter beaucoup d’ingéniosité.
Un début bien laborieux
Comme souvent, j’ai bien du mal à résister aux défis que je me lance et, après avoir profité des remontées mécaniques pour ruminer quelques idées préliminaires, j’ai très vite commencé à les tester en vrai une fois de retour à la maison. Mais la difficulté du problème dépassait largement mes attentes. Je ne vous cache pas que mes premiers essais étaient réellement minables. Imaginez mes premières itérations avec une toute petite grille de 9 cases sur 9 qui se remplissait laborieusement jusqu’à moitié, puis qui itérait interminablement sur toutes les combinaisons possibles de ces 4 ou 5 mots, sans jamais arriver à en placer un 6ème. Le quatrième mot était au mieux mis à jour toutes les demi-heures et, à ce rythme, je voyais mal la grille remplie avant un million d’années. Alors je ne vous parle même pas de grilles de taille plus importante, comme le format 17x17 que l’on retrouve le plus souvent. Certes, l’algorithme était correct d’un point de vue formel, dans le sens où il finirait par trouver une solution à force de passer en revue toutes les possibilités, mais d’un point de vue pratique c’était désastreux.
Il m’apparut vite que plusieurs problèmes devaient être surmontés avant d’aboutir à quelque chose qui tienne la route, et que chacun de ces points était déterminant pour atteindre le Graal du générateur performant.
- Comment encoder le dictionnaire de mots et comment être efficace pour trouver des candidats à placer sur la grille ?
- Quelle stratégie employer pour placer et tester les mots sur la grille ?
- Comment éviter au maximum de tester des combinaisons inutiles ou, en d’autres mots, comment élaguer au maximum l’arbre des possibilités ?
Je vais aborder ces trois questions l’une après l’autre par la suite, mais parlons tout d’abord du backtracking lui-même pour bien cerner le contexte dans lequel elles s’inscrivent.
La longue voie du backtracking
Comme cela est mentionné sur Wikipedia, le backtracking désigne une famille d’algorithmes permettant de résoudre des problèmes de satisfaction de contraintes. Cela tombe bien, car c’est justement ce de quoi il s’agit ici: une grille vierge doit être remplie de lettres sous la contrainte que leurs séquences, prises horizontalement ou verticalement, correspondent toujours à un mot se trouvant dans une liste préétablie. Son implémentation naïve consiste simplement à énumérer toutes les possibilités jusqu’à en trouver une ne violant aucune règle imposée.
Pour fixer les idées, je vous propose d’ignorer les cases noires dans un premier temps et de se concentrer sur la génération de grilles carrées parfaites, c’est à dire ne contenant que des lettres. Ce problème offre l’avantage de pouvoir à la fois illustrer simplement le principe du backtracking, mais aussi de se rendre compte de la complexité abyssale du processus pour peu que l’on s’y essaie avec une approche brutale et naïve.
Commençons par un problème très simple permettant d’énumérer facilement toutes les solutions: considérons une grille de 3x3 à remplir avec le dictionnaire contenant cette copieuse liste de mots: « QUE », « UNS », « EST » et « TES ».
L’idée du backtracking revient simplement à placer les éléments les uns à la suite des autres, en effectuant chaque fois un choix parmi tous ceux respectant les contraintes désirées. Bien sûr, il se peut qu’il n’y ait parfois aucune possibilité, ce qui implique de changer un élément placé précédemment pour permettre d’énumérer de nouvelles combinaisons. Si ce dernier élément vient lui aussi à être épuisé, alors on remontera encore d’un cran dans la pile d’éléments déjà en place, et ainsi de suite. Cette méthode se contente donc d’énumérer tous les cas possibles jusqu’à tomber sur une solution par hasard. Dans le cas de notre petit exemple, l’arbre des combinaisons et la manière d’itérer à travers lui sont donnés ci-dessous.
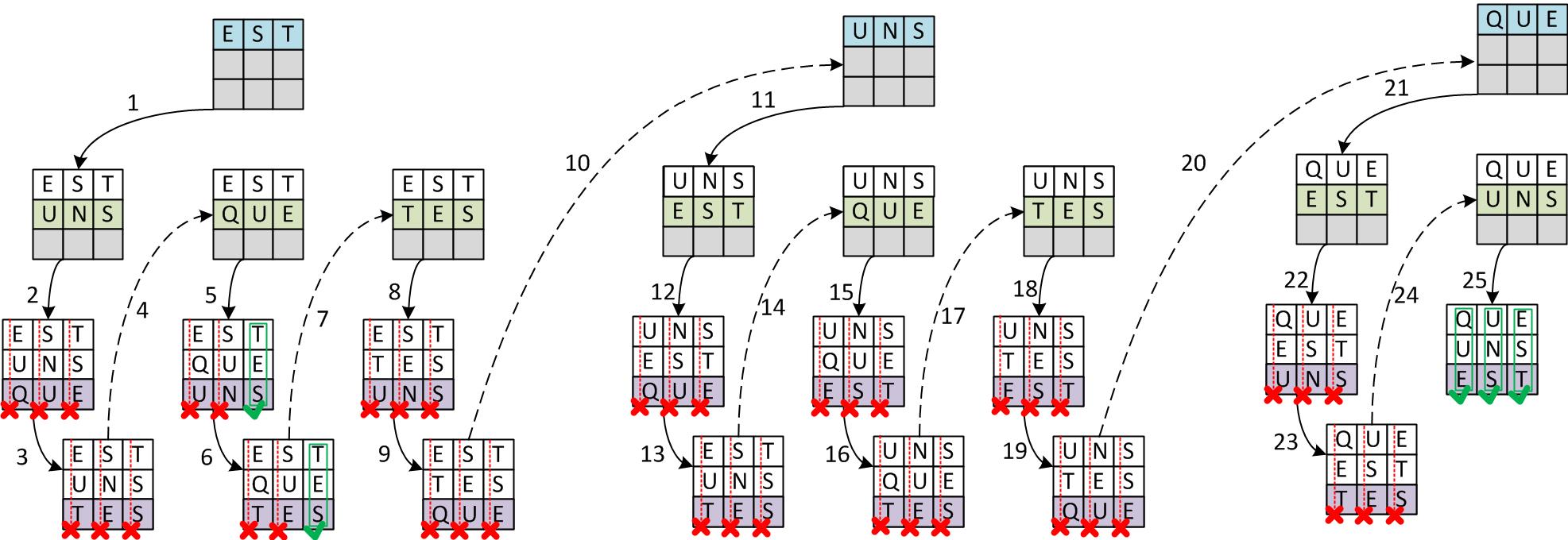
Illustration du cheminement du backtracking. Dans cet exemple, il se borne à tester toutes les combinaisons possibles.
Pour cet exercice, nous essayons de placer itérativement trois mots horizontalement, de haut en bas. Dès que le troisième mot est placé, nous vérifions si les trois mots verticaux alors formés sont dans le dictionnaire. Si ce n’est pas le cas, l’algorithme ôte ce dernier de la grille et choisit une nouvelle possibilité pour le deuxième emplacement.
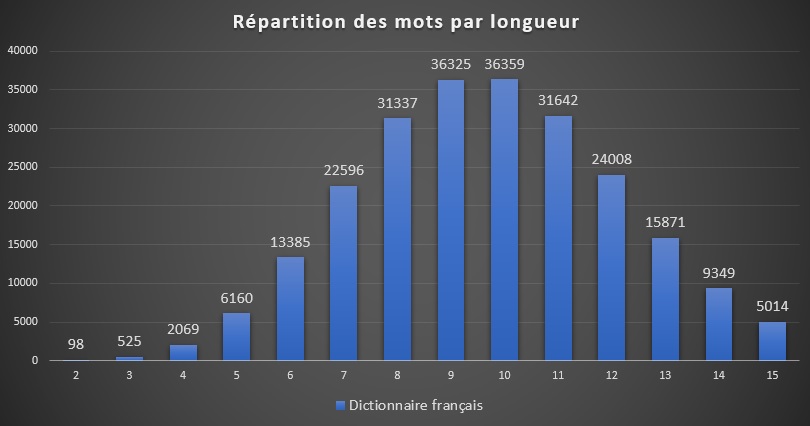
La procédure est systématique et garantit de trouver la solution. Essayons toutefois d’évaluer la difficulté d’un tel problème en fonction d’une taille de grille $S$ et d’un dictionnaire contenant $N$ mots de taille $S$. Histoire de fixer les idées, voici la répartition des mots en fonction de leur longueur dans le dictionnaire français que j’utilise.
Il est nécessaire d’empiler $N$ mots l’un sur l’autre avant de pouvoir vérifier si chacun des $N$ emplacements verticaux contiennent par hasard un mot valide. Il est possible d’estimer cette probabilité aisément pour peu que l’on ignore les corrélations entre séquences de lettres. Ainsi si nous prenons deux mots $w_1$ et $w_2$ au hasard dans le dictionnaire, la probabilité de coïncidence entre la $i^{ème}$ lettre du premier et la $j^{ème}$ lettre du second se calcule par :
$$p_{co}=P(w_1[i]=w_2[j])=\sum_{l=1}^{26}f(l)^2,$$
dans laquelle $f(l)$ correspond à la fréquence d’occurrence de la $l^{ème}$ lettre de l’alphabet. Cette fréquence se détermine simplement par inspection des mots du dictionnaire, comme avec l’histogramme qui suit.
Ce qui donne une probabilité de coïncidence $p_{co}$ de 7,8%. Un mot de taille $N$ dans une colonne sera alors valide si et seulement si cette probabilité nous est favorable $S$ fois de suite pour n’importe lequel des $N$ mots valides. La probabilité $p_v$ de trouver un mot correct dans n’importe lequel des emplacements verticaux est alors de:
$$p_v=1- (1 - p_{co}^S)^N $$
Quant à la probabilité $p_g$ que la grille complète soit correcte, elle est donnée par:
$$p_g={p_v}^S = N^S.{p_{co}}^{S^2}$$
Nous pouvons tout de suite constater que cette formule n’a pas l’air très favorable pour les grilles de grandes dimensions. Par contre, et c’est logique, plus le dictionnaire contient de mots plus nos chances de trouver un arrangement correct sont importantes. Mais pour bien se rendre compte de ce que cette formule représente, mettons toute de suite quelques chiffres par-dessus:
| $S$ | $N$ | $p_g$ | Nombre de grilles | Durée moyenne de résolution |
|---|---|---|---|---|
| 5 | 6160 | $10^{-8.7}$ | $10^{19.0}$ | 2 minutes |
| 6 | 13385 | $10^{-15.0}$ | $10^{24.8}$ | 35 années |
| 7 | 22596 | $10^{-23.7}$ | $10^{30.5}$ | 10 milliards d’années |
| 8 | 31337 | $10^{-34.8}$ | $10^{36.0}$ | 1000 milliards de milliards d’années |
| 9 | 36325 | $10^{-48.5}$ | $10^{41.0}$ | ??? |
| 10 | 36359 | $10^{-65.0}$ | $10^{45.6}$ | :'-( |
Les deux premières colonnes donnent la taille de la grille considérée et le nombre de mots de cette longueur s’y rapportant. La troisième colonne donne la probabilité qu’une grille assemblée au hasard en empilant $S$ mots soit valide, tandis que la quatrième donne le nombre total de grilles qu’il est possible de générer de la sorte. Enfin, la dernière colonne estime le temps moyen nécessaire pour trouver une grille correcte à raison d’un million de grilles testées par seconde.
Une première constatation intéressante vient de la comparaison du nombre de grilles qu’il est possible de générer avec la probabilité que l’une d’elles soit une solution. Avec le dictionnaire utilisé pour créer cette table, il apparait avec certitude qu’aucune grille parfaite de taille 9 ne peut être générée, le nombre de combinaisons étant 10 millions de fois trop faible que pour espérer en trouver une. Quant aux grilles de taille 8, elles devraient contenir une quinzaine de solutions.
Le deuxième point important concerne le nombre pantagruélique de grilles à tester avant de pouvoir espérer trouver une combinaison gagnante. Pour une grille de taille 8, cette valeur tourne autour de $10^{35}$ grilles, ce qui s’apparente à trouver le bon grain de sable parmi un volume de sable fin équivalent à celui de la terre. Cette analogie plus que parlante montre de manière évidente que la méthode proposée ici nécessite quelques ajustements, afin de pouvoir générer des grilles parfaites en moins de mille-milliards de milliards d’années.