Wizium - Mon générateur de mots croisés
De la bonne façon de paver sa grille
La méthode utilisée précédemment pour remplir la grille se voulait excessivement naïve, car il est tout à fait catastrophique de ne tester la validité de la solution qu’une fois tous les mots placés. Le problème étant combinatoire, la nature exponentielle des combinaisons de mots s’affiche comme autant de branches, branchettes et puis brindilles se subdivisant effroyablement rapidement. Aussi vaut-il mieux se rendre compte le plus tôt possible que la voie choisie n’aboutira à aucune solution, de manière à couper la branche morte dès le début et ne pas perdre du précieux temps de calcul au fin fond de son arborescence.
Reste maintenant à savoir quelle est la manière la plus efficace pour procéder, de façon à anticiper aussi vite que possible une quelconque situation de blocage. Je ne prétends pas détenir la réponse ultime à cette question et je me contenterai de présenter deux méthodes possibles, l’une d’elles est celle implémentée dans Wizum.
Première méthode: le tressage
Cette technique est assez naturelle et consiste à alterner la pose des mots horizontalement et verticalement, de haut en bas et de gauche à droite. L’entrelacement des mots est alors maximal et permet de détecter très tôt l’impossibilité de placer un $n^{ème}$ mot. Le cas échéant, il suffira alors de modifier le mot précédent au niveau de la lettre qui a conduit à ce blocage.
Dans l’exemple ci-dessus, la pose du troisième mot vertical avec CREOLE empêche ensuite de placer le quatrième mot horizontal. Il n’existe en effet aucune solution de six lettres commençant par REO. Cela invalide le mot précédent et conduit immédiatement à le remplacer par quelque chose ne contenant pas de O sur la quatrième rangée. Toutes les cases vides de la grille sont alors autant de combinaisons de mots qui ne devront pas être testées.
Essayons maintenant d’évaluer le gain que cette méthodologie peut offrir. On peut l’étudier en l’abordant comme une chaine de Markov discrète, c’est-à-dire que l’algorithme de pavage de la grille peut être assimilé à un processus stochastique dont l’état correspond uniquement à l’indice du mot à placer. Le succès ou l’échec de cette opération conduit soit à avancer au mot suivant ou, au contraire, à reculer pour modifier le précédent. Ce processus n’est pas réellement homogène, car techniquement, les probabilités de transitions ne dépendent pas seulement de la partie de la grille que l’on essaie de remplir, mais aussi de toutes les combinaisons de lettres qui ont déjà été épuisées. Nous nous contenterons toutefois de cette approximation dans la mesure où nous voulons seulement estimer l’ordre de grandeur du gain apporté par cette approche.
Pour ce faire, désignons par ${w_h}_i$ les $S$ emplacements horizontaux et, de la même manière, par ${w_v}_i$ pour les emplacements verticaux. La probabilité qu’il existe un mot du dictionnaire pour remplir chacun d’eux est donnée par:
$${p_{h}}_i = 1 - (1 - {p_{co}}^i)^N$$
$${p_{v}}_i = 1 - (1 - {p_{co}}^{i+1})^N$$
avec $i=0…S-1$. Ces formules traduisent simplement la probabilité qu’un certain nombre de lettres assemblées au hasard correspondent à une partie de mot valide. Plus $i$ augmente, plus les chances diminuent à cause du nombre croissant de lettres avec lequel il faut composer. Nous pouvons alors modéliser le processus de backtracking par cette chaine de Markov.
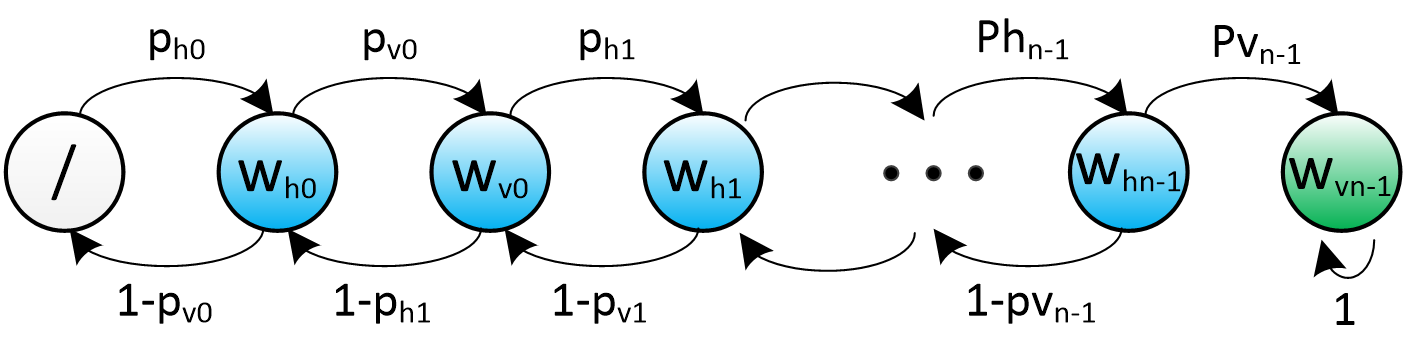
Chaine de Markov modélisant les probabilités de trouver un mot adéquat pour paver chacun des emplacements de la grille.
Sans trop entrer dans les détails mathématiques, un processus de Markov peut s’étudier au travers des propriétés de sa matrice de transition $P$. Celle-ci est construite de telle sorte que chaque élément $(P)_{ij}$ soit égal à la probabilité de transition entre l’état $i$ et l’état $j$.
$$P=\begin{pmatrix} 0 & 1-{p_v}_0 & 0 & 0 & 0\newline {p_h}_0 & 0 & \ddots & 0 & 0\newline 0 & {p_v}_0 & 0 & 1-{p_v} _ {S-1} & 0\newline 0 & 0 & \ddots & 0 & 0 \newline 0 & 0 & 0 & {p_v} _ {S-1} & 1 \end{pmatrix}$$
de telle sorte que si $\phi(n)$ représente la distribution de probabilité de l’état du processus au temps $n$, alors la distribution au pas suivant sera donnée par:
$$\phi(n+1) = P. \phi(n)$$
Le dernier état appelé un état absorbant, car il correspond à la construction d’une grille complète valide et stoppe la recherche. Cela peut se voir sur le graphe à cause de l’unique transition de probabilité 1 qui cycle sur cet état final. Cette propriété se constate aussi dans la dernière colonne de la matrice $P$ qui ne permet pas de redistribuer les probabilités autre part que dans le dernier état. A l’inverse, tous les autres états sont dit transitoires, dans la mesure ou rien de garantit que l’algorithme les traversera plus d’une fois. La valeur qu’il est alors particulièrement intéressant d’étudier concerne le temps passé en moyenne dans ces états transitoires avant d’atteindre l’état final.
Pour y arriver, il nous faut d’abord réécrire la matrice $P$ en mettant en évidence cette distinction, grâce à la matrice carrée $Q$ capturant cet aspect transitoire, ainsi qu’au vecteur $R$ représentant l’état absorbant.
$$P=\begin{pmatrix} Q & \boldsymbol{0}\newline R & 1\newline \end{pmatrix}$$
Cela permet ensuite de calculer la matrice $N = (I-Q)^{-1}$ grâce à laquelle on peut trouver la durée moyenne du transitoire, ou dit autrement, le nombre de pas moyen de l’algorithme de backtracking (suivez ce lien pour plus d’information à ce sujet).
Examinons maintenant les nouvelles estimations du nombre de pas nécessaires pour résoudre nos grilles parfaites de différentes tailles, afin d’apprécier le gain apporté par cette nouvelle méthode.
| $S$ | Nombre de grilles | #pas, naïf | #pas, tressage | Résolution |
|---|---|---|---|---|
| 5 | $10^{19}$ | $10^{8.7}$ | $10^{3.4}$ | 1ms |
| 6 | $10^{24.8}$ | $10^{15.0}$ | $10^{6.3}$ | 2s |
| 7 | $10^{30.5}$ | $10^{23.7}$ | $10^{11}$ | 1 journée |
| 8 | $10^{36.0}$ | $10^{34.8}$ | $10^{17.8}$ | 20.000 ans |
La dernière colonne estime à nouveau le temps de résolution à raison d’un million de tests par seconde. Il va sans dire que le progrès est spectaculaire, la résolution d’une grille 7x7 pouvant maintenant s’envisager sans problème, en passant d’un temps de 10 milliards d’années (ce qui n’est pas loin de l’âge de l’univers) à seulement une journée. Les grilles 8x8 restent toutefois encore hors de portée avec cette méthode, du moins si l’on se cantonne à l’usage d’un PC conventionnel.
Deuxième méthode: l’échafaudage
La technique que je m’apprête à décrire constitue la base de l’algorithme implémenté dans Wizium. Elle résulte avant toute chose d’une longue recherche ponctuée de beaucoup d’essais et de nombreuses erreurs, et pas de l’analyse que vous êtes en train de lire, car cette dernière est arrivée bien plus tard. Malgré son élaboration empirique, son principal avantage est de ne pas souffrir des mêmes faiblesses que la méthode précédente. Elle est beaucoup plus directe et anticipe mieux les problèmes. Pour s’en rendre compte, commençons par jeter un oeil à la construction de la grille qui suit:

Construction pathologique par entrelacement vertical horizontal des mots. C'est seulement au dernier stade de l'algorithme que l'impossibilité de la dernière colonne est détectée.
Cette construction pathologique a été imaginée sur mesure, mais illustre néanmoins une tare inévitable de la méthode de tressage: lorsque l’on place les derniers mots, le succès de l’opération joue tout sur la chance et rien sur l’anticipation. C’est ce qui peut se voir dans cet exemple, la pose du deuxième mot horizontal engendre un blocage inévitable, car il empêche de placer ensuite un mot verticalement sur la dernière colonne. Mais rien dans l’algorithme ne permet ensuite de détecter cette impasse et celui-ci continuera laborieusement à construire une grille qui est vouée à l’échec. C’est seulement lors de la pose du dernier mot que la procédure commencera à revenir en arrière pour résoudre la situation, et il devra pour ça défaire presque toute la grille.
Pour éviter ce genre de contrariétés, il est nécessaire et suffisant de vérifier qu’il est encore possible de placer un mot verticalement sur chaque colonne à chaque fois que l’on choisit un mot horizontal. Mais en procédant de la sorte, il n’est en fait même plus nécessaire de placer aucun mot verticalement. L’empilage de mots horizontaux suffit, dans la mesure où celui-ci se réalise de manière éclairée: l’algorithme s’assure continuellement que l’on n’aura pas de mauvaise surprise à la fin. Il n’est donc plus question ici de jeter les mots en vracs pour espérer en sortir une grille valide, il s’agit plutôt d’empiler les mots avec soin. Il est bien sûr possible que, à un moment, aucun mot du dictionnaire ne satisfasse cette contrainte. Mais dans ce cas, le blocage est identifié au plus tôt et permet tout de suite de revenir en arrière, sans s’embarquer dans une recherche stérile. Cette méthode est illustrée dans l’animation qui suit.

Échafaudage méthodique des mots horizontaux, en vérifiant systématiquement les emplacements verticaux.
Outre sa capacité d’anticipation, cette méthode nécessite de placer seulement $S$ mots sur la grille, contre $2.S$ mots pour la méthode de tressage. Cela implique que le graphe de Markov correspondant s’en trouve raccourci et, moyennant que les probabilités de transition soient favorables, puisse s’en trouver plus facile à traverser.
Étudions donc ces probabilités de transition. L’approche est la suivante: un mot horizontal peut être placé s’il existe au moins un mot vertical compatible sur chacune des colonnes traversées. Il convient tout d’abord de se pencher d’un peu plus près sur ce nombre de mots compatibles. Il est certain que, plus je m’avance dans la construction, plus ce nombre diminue du fait de la longueur plus élevée des préfixes correspondants. Par exemple, lorsque je pose le mot BRELER, je dois vérifier qu’il existe bien un mot commençant par HAB dans la première colonne. Ce nombre de possibilités est plus élevé que lorsque je pose le mot ETETER et que j’aie à vérifier qu’il existe un mot débutant par HABLE.
Le nombre moyen de mots disponibles, étant donné la longueur d’un préfixe, se trouve simplement en compilant quelques statistiques sur le dictionnaire utilisé. Ce script permet de réaliser ce travail et la figure qui suit en illustre quelques chiffres.
Définissons donc la fonction $M (S, i)$ exprimant le nombre moyen de mots disponibles étant donné une longueur de préfixe $i$. Celle-ci nous permet alors de calculer la probabilité qu’une lettre d’un mot horizontal placé au niveau $i$ permette toujours de poser un mot verticalement par-dessus.
$${p_ {co}}_i = 1 - (1-p _{co})^{M(S, i)}$$
La probabilité qu’un mot donné soit compatible sur chaque colonne est alors donnée par ${{p_ {co}}_i}^S$, ce qui permet finalement de calculer la probabilité de pouvoir placer un mot au niveau $i$:
$${p_ {h}}_i = 1 - (1-{{p _{co}} _i}^S )^N$$
Avant d’aller plus loin, il est intéressant de comparer les deux méthodes au niveau de leurs probabilités de transition avec des valeurs concrètes. Celles-ci sont reprises dans la table qui suit pour une grille de 6x6 cases. Non seulement la technique d’échafaudage requiert moins d’étapes, mais les probabilités de pose sont aussi plus élevées.
| Étape | Tressage | Échafaudage |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 1 | 1 |
| 4 | 1 | 1 |
| 5 | 1 | 0.47 |
| 6 | 0.998 | 0.043 |
| 7 | 0.998 | |
| 8 | 0.39 | |
| 9 | 0.39 | |
| 10 | 0.038 | |
| 11 | 0.038 | |
| 12 | 0.003 |
Muni de ces nouvelles probabilités, nous pouvons à nouveau calculer l’espérance du transitoire afin d’obtenir un ordre de grandeur du nombre de pas nécessaires pour résoudre la grille par cette deuxième approche. Il est toutefois important de souligner qu’il est ici nécessaire de corriger les valeurs obtenues. En effet, les probabilités de transition témoignent ici de la possibilité qu’il existe un mot compatible avec chacune des colonnes traversées, mais encore faut-il trouver ce mot ! Ce n’est en aucun cas immédiat puisque cela peut nécessiter d’en tester plusieurs pour y parvenir. Il demeure tout de même possible d’y arriver intelligemment en gardant le compte de toutes les lettres incompatibles, ce qui permet d’épuiser tout le dictionnaire en un maximum de $26.S$ étapes.
La table qui suit permet de comparer le nombre de pas propres aux deux méthodes exposées avec, pour la dernière, une correction d’un facteur pifométré à $10.S$.
| $S$ | Nombre de grilles | #pas, tressage | #pas, échauf. | Résolution |
|---|---|---|---|---|
| 5 | $10^{19}$ | $10^{3.4}$ | $10^{2.8}$ | 0,5 ms |
| 6 | $10^{24.8}$ | $10^{6.3}$ | $10^{3.8}$ | 6 ms |
| 7 | $10^{30.5}$ | $10^{11}$ | $10^{5.7}$ | 0,5 sec. |
| 8 | $10^{36.0}$ | $10^{17.8}$ | $10^{8.5}$ | 5 min. |
Bien que cette étude soit théorique, le nombre de pas moyen pour résoudre ces grilles parfaites dans Wizium est très proches des valeurs affichées ici. Cela montre bien à quel point le choix de l’algorithme est primordial lorsque la taille du problème à traiter est grande. Pour les grilles de 8x8, il nous a permis de passer d’une résolution en mille-milliards de milliards d’années à 20.000 ans, puis à une poignée de minutes. Il s’agit d’une accélération vertigineuse de pas moins de 26 ordres de grandeur, ce qui est plus ou moins équivalent à réduire la taille d’une galaxie à celle d’une ville puis à celle d’une bactérie.

